
1
1
1
1
2
1
Triángulo de
Tartaglia
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
...
...
...
...
...
...
...
1
1
2
3
5
8
13
...
Números de
Fibonacci
FIBONACCI Y LA RAZÓN ÁUREA
Dr. Baldovino Lamirata Carigli
Facultad de Ciencias, ESPOCH
baldovinol@hotmail.com
R
esumen
En el artículo se muestra que la relación existente entre los números de Fibonacci y la razón áurea
es que la sucesión de las razones de dos sucesivos números de Fibonacci converge justo al valor de
la razón áurea.
Además se justifica la importancia de la razón áurea por sus innumerables aplicaciones operadas
tanto en la naturaleza misma como por el hombre.
Palabras claves: Números de Fibonacci, razón áurea
A
bstract
The article shows that the relationship between Fibonacci numbers and the golden section is that the
sequence of ratios of two successive Fibonacci numbers converges fair value of the golden ratio.
It also justifies the importance of the golden section for countless applications operated by the very
nature and by man.
Keywords: Fibonacci number, golden ratio
INTRODUCCIÓN
En el artículo titulado Sucesión
de presentado en la revista
Nuestra Ciencia n.º 8, de 2006, de la Fa-
cultad de Ciencias de la PUCE, aseveré
que los números de Fibonacci y la razón
áurea tienen mucho en común. Continúo
entonces esta reflexión, recomendando
a los interesados leer aquel artículo; de
manera que supongo conocidos los nú-
meros de Fibonacci y algunas de sus
propiedades, descritas allí.
1. LA SUCESIóN DE LAS RAZONES Rn
Por comodidad del lector, se reportan
los primeros términos de la sucesión de
Fibonacci:
Figura 1. Números de Fibonacci frente
Triángulo de Tartaglia

R
i
n n
F
F
0
1
0
Excepto por los dos primeros términos,
no se necesita recordar los otros porque
son la suma de los dos anteriores:
Fn = F
+ F
, n > 2
resulta:
= 1 , R
=
1
1 + R
1
=
1 + 1
1
1
1 1
Obsérvese que los números de Fibonac-
ci también se pueden construir emplean-
R2
=
1 + R
=
, R =
=
1
3
1 + R 1
do el Triángulo de Tartaglia, como se
muestra en la figura 1.
1
1 +
2
1 +
1 + 1
1 +
1
Construyamos ahora las razones entre
1 + 1
un término y el siguiente:
Se genera una fracción continua
1
que converge al límite
de las razones entre los sucesivos números de Fibonacci.
El número a así definido:
1
1 2 3 5
8 13 21 34 55 89
2 3 5 8 13 21 34 55 89 144
1
a =
cuyo valor en notación decimal es:
1 0,5 0,6 0,6 0,625
0,619...
1 + a
genera por sustitución repetida la siguiente fracción con-
tinua:
1 1 1
a =
1 + a
=
1
=
1
= ...
Estas razones tienden a estabilizarse al-
rededor de un valor poco superior a 0,6.
Encontrémoslo.
Hay una fórmula recursiva para gene-
1 + 1 +
1 + a
1 +
1
1 + a
rar las fracciones. Indiquemos por R
n+1
y por supuesto es el límite de la fracción misma.
la razón entre el número (n+1)-ési-
Ahora bien, esta fracción continua converge al mismo
mo y el (n+2)-ésimo de Fibonacci; se
valor de la sucesión de las razones R y por tanto a es
cumple:
F
n+1
R = =
F
n+1
1
=
=
el límite de las razones entre los sucesivos números de
Fibonacci:
n+1
F
F + F
F + F
a = lim
n+2
n+1 n
n+1 n
F
n+1
El valor a se calcula en el modo siguiente. Se cumple:
1 1
= a(1 + a) = 1
1 +
Al poner:
n
n+1
1 + R
n
luego:
a
2
+ a 1 = 0
ISSN 1390-5740
Número 12 Vol. 2 (2014)
ISSN 2477-9105
Lamirata
luego:
-1 ±
5
a =
2
Se prueba que AB es la media propor-
cional entre toda la secante AD y la parte
externa AE:
AD : AB = AB : AE.
Por ser a el límite de una sucesión de términos positivos,
su valor no puede ser negativo, luego queda la sola solu-
ción positiva:
5 - 1
y por tanto:
(AE + ED) : AB = AB : AR.
Sigue:
a =
2
2. LA RAZÓN ÁUREA
(1)
(AE + ED AB) : AB = (AB AR) : AR
AR : AB = RB : AR AB : AR
= AR : RB
Existe un rectángulo tan armónico que se merece el ca-
lificativo de es el que tiene las medidas de los
lados en una razón especial, indicada por , la inicial del
artista ateniense Fidia, que vivió en el siglo V antes de
Cristo.
luego AR es la razón áurea de AB. Por
ende, el siguiente es un rectángulo áureo:
El rectángulo aparece en las construcciones griegas que
A
B
se consideran como el Partenón en Atenas y el
r
templo de Poseidón en Phestum, como también en las
esculturas y en la naturaleza.
La razón áurea es la media proporcional entre un seg-
mento y la parte que queda.
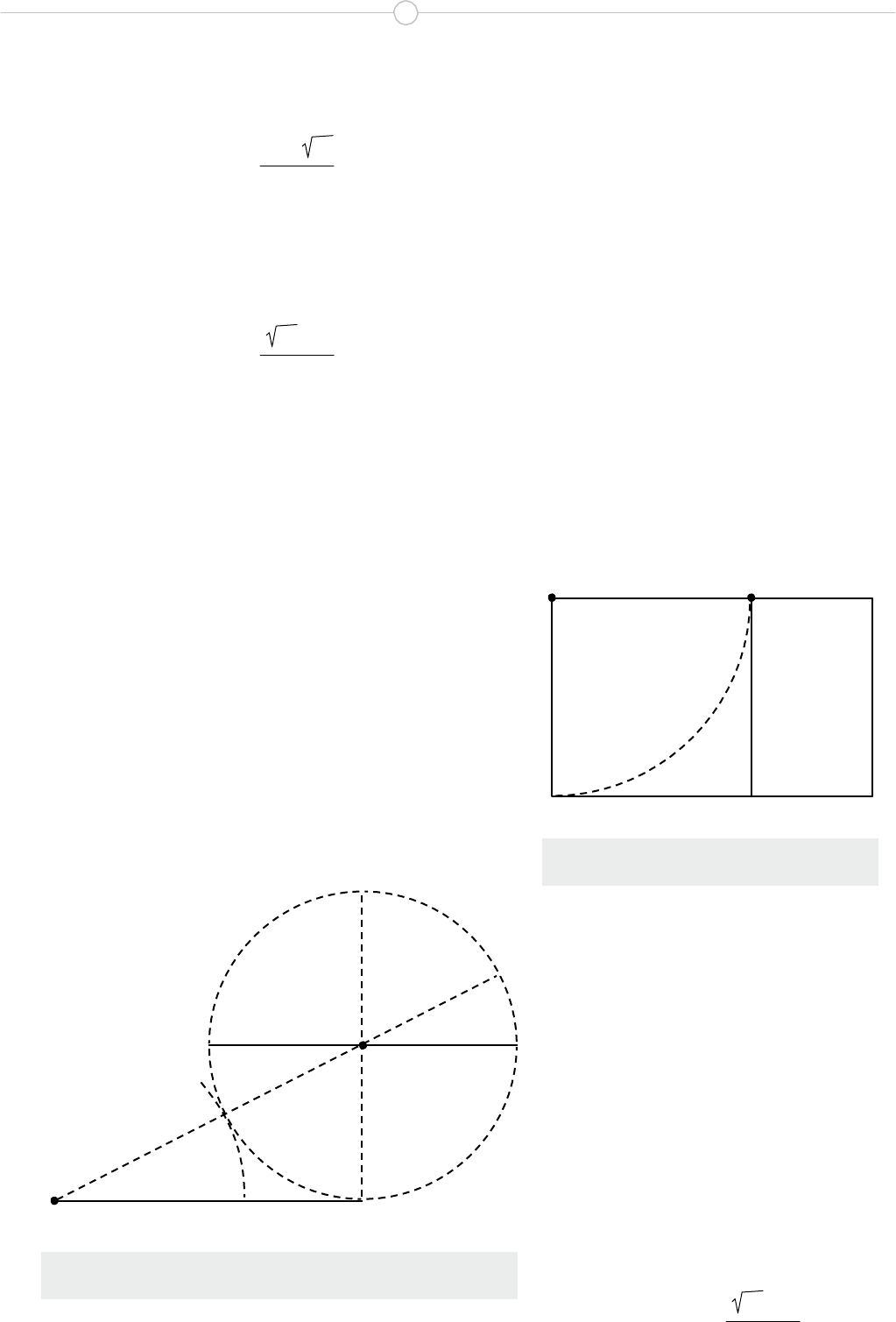
Se construye de la manera siguiente. Dado el segmento
AB, se traza la circunferencia de diámetro igual a AB y
tangente al segmento en B, luego se traza la secante por
A y por el centro C de la circunferencia:
d
Figura 3. Rectángulo áureo
Si se asume igual a 1 la medida del seg-
d
mentoAB,es:
C
Sigue:
E
1 : = .
2
=
luego:
A
r
B
Figura 2. Construcción de la razón áurea
2
+ = 0.
Por (1), el número positivo que solucio-
na a esta ecuación es
5 - 1
2
0
n
1
{
1
1
2
3 -
2
3
Por ende:
5 - 1
=
2
Generalmente este proceso de construcción de rectángu-
los y cuadrados acaba. ¿Hay un valor de la razón entre
las medidas del rectángulo dado: x / x1, por el cual el
proceso no tenga fin?
Obtengamos una expresión recursiva de x . Considérense
Por ende, el rectángulo áureo de base
las dos soluciones de la ecuación a
2
+ a 1 = 0, que como
ya sabemos son:
AB tiene altura AD =
5 - 1
2
AB.
5 - 1 5 - 1
Y aquí el nexo entre los números de Fi-
bonacci y la razón áurea:
a =
2
< 1
,
a
2
=
2
< -1
la sucesión de las razones rn
de los números de fibonacci
converge a la razón áurea φ.
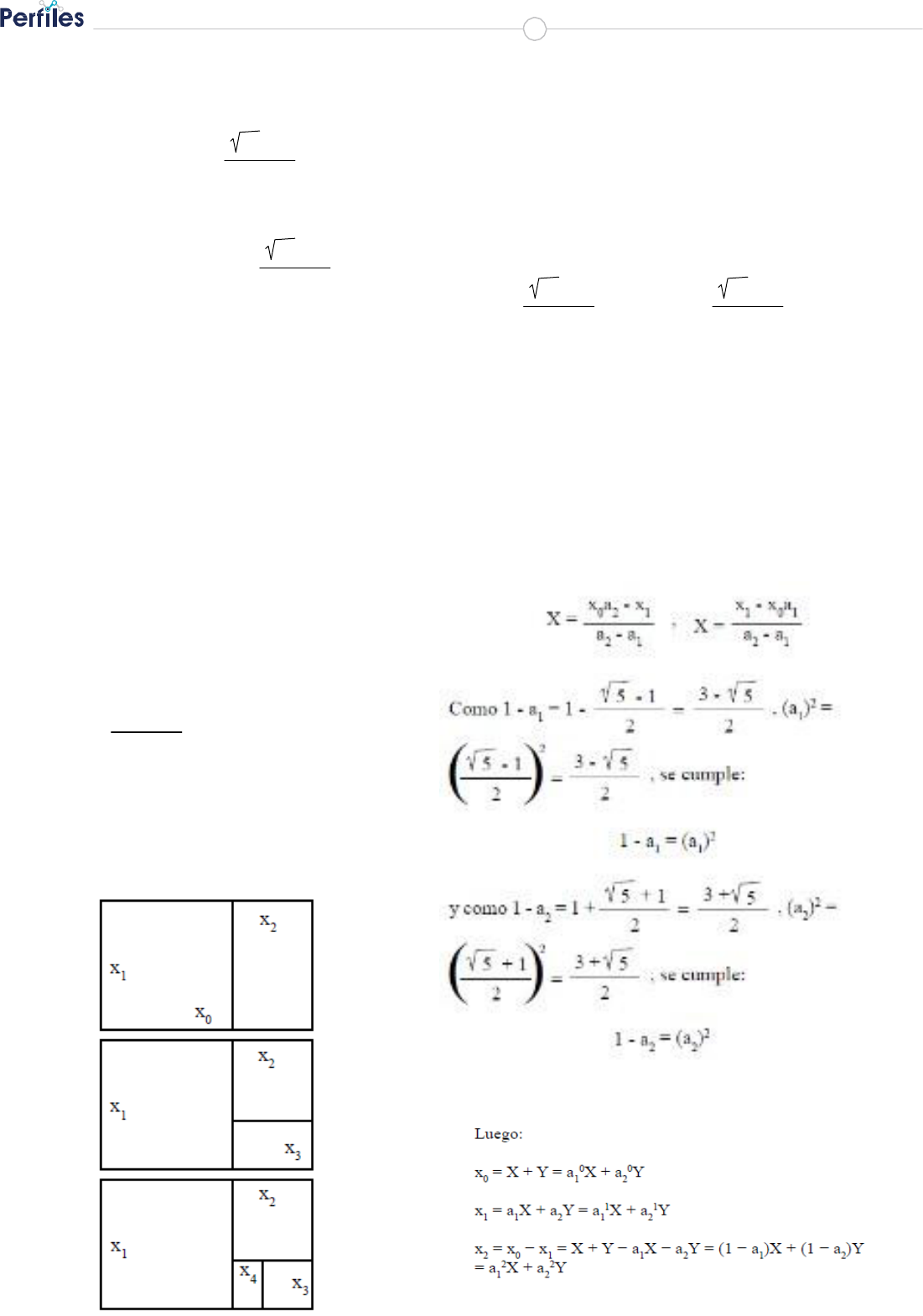
Otra característica: considérese un rec-
tángulo de medidas x y x , con x < x <
0 1 1 0
2x
1
. Entonces se puede trazar en el inte-
rior del rectángulo un cuadrado de lado
de longitud x y queda un rectángulo de
lado mayor de longitud x y de lado me-
nor de longitud x
2
= x
0
x
1
.
Si x < x < 2x , se puede trazar en el
y el sistema en las incógnitas X, Y:
X + Y = x
0
a
1
X +a
2
Y = x
1
cuyas soluciones son:
2 1 2
interior del segundo rectángulo un cua-
drado de lado de longitud x y queda un
rectángulo de lado mayor de longitud x
y de lado menor de longitud x = x x .
Si x < x < 2x , se puede trazar en el in-
terior del tercer rectángulo un cuadrado
de lado de longitud x y queda un rectán-
gulo de lado mayor de longitud x
3
y el
menor de longitud x
4 2 3
ISSN 1390-5740
Número 12 Vol. 2 (2014)
ISSN 2477-9105
Lamirata
n
n
x = x x = a X + a Y a
2
X a
2
Y = (a a
2
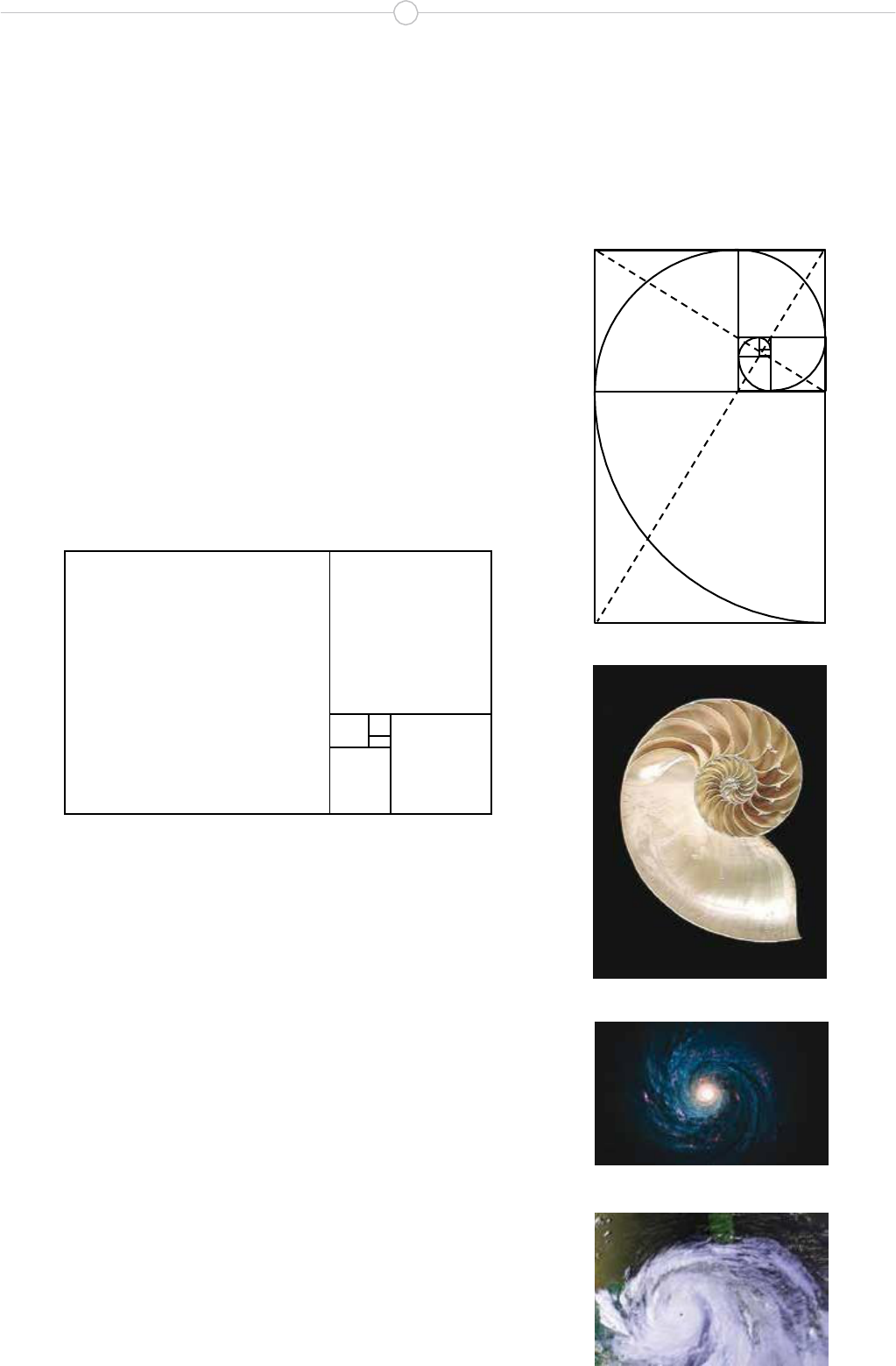
)X + (a Se construye una parte conectando los vér-
3 1 2 1 2 1 2 1 1 2
a
2
)Y = a
3
X + a
3
Y tices opuestos de todos los cuadrados ob-
2 1
2
tenidos mediante arcos de circunferencia.
Es una de las espirales arquetipo de ga-
x = x x = a
n-2
X + a
n-2
Y a
n-1
X a
n-1
Y = (a
n-2
laxias, formaciones huracanadas, conchas:
a
n
n-1
)X
n-
+
2 (a
n
n
-
-
2
11
a
n-1
)Y = a
2
n
X + a
n
1
Y
2 1
1 2 2 1 2
Para que el proceso de recorte sea infinito, los x tienen
que seguir siendo positivos. Ellos son iguales a la suma
a X + a Y de la cual el primer sumando siempre es positi-
1n 2n
vo y menor que X, el segundo es alternativamente positivo
y negativo según el valor de n, mayor que Y y creciente en
valor absoluto con n. Entonces para que los x sean todos
positivos, debe ser Y = 0, luego debe ser x1 = a11X = a1x0,
esto es, la altura del rectángulo debe ser la razón áurea de
la base, o sea el rectángulo debe ser áureo.
Una última nota. ¿Por qué a la razón áurea se la llama así?
Hasta la llamaron divina Es que ella está
presente en muchas obras de la naturaleza y del hombre.
Vimos que a partir de un rectángulo áureo, recortando un
cuadrado de lado igual al lado menor, se obtiene un rec-
tángulo más pequeño símil al primero, luego áureo; del
cual recortando un cuadrado de lado igual al lado menor,
se obtiene un tercer rectángulo aun más pequeño, símil a
los anteriores, luego áureo; y así sucesivamente.
Asimismo, construyendo sobre el lado mayor del primer
rectángulo un cuadrado, este determina con el primer rec-
tángulo áureo todavía un rectángulo áureo, sobre el cual
operando de manera análoga se obtiene todavía un rectán-
gulo áureo más grande, y así sucesivamente.
Ahora, construyendo los rectángulos siempre de la misma
parte, los puntos de corte a, b, d, e, f, g, pertenecen a
una espiral logarítmica, con el polo punto de intersección
de la diagonal común a los rectángulos horizontales con la
diagonal común a los rectángulos verticales. Esta espiral
logarítmica especial se llama espiral áurea.

Asimismo, si contamos las hojas sucesivas
de un tallo hasta encontrar una con la mis-
ma orientación de la primera, el número
que se obtiene es un número de Fibonacci.
Finalmente, la razón áurea está presente
en muchas obras arquitectónicas y en el
arte, como demostración de que los gran-
des artistas conocen la Geometría:
RECOMENDACIONES
En la Red hay muchos sitios que hablan acerca de la suce-
sión de Fibonacci y de la razón áurea. Para ampliar o profun-
dizar estas notas, se recomienda a estudiantes, arquitectos,
profesionales de la imagen visitar los sitios que aparecen en
la bibliografía.
RB
eibflieorgernacfiíascomplementaria
1. Corbalán F. La Proporción Áurea. RBA Coleccionables S. A.; 2010.
2. Ghyka M. El número de Oro. I Los Ritmos. II Los Ritos. Madrid, España: Ediciones Apóstrofe,
S. L.; 2006.
3. Ghyka M. La Divina Proporción. Tres Cantos. Ediciones Akal, S. A.; 1991.
ISSN 1390-5740
Número 12 Vol. 2 (2014)
ISSN 2477-9105