
12
BANDAS DE CONFIANZA BOOTSTRAP
EN REGRESIÓN POLINÓMICA
Lourdes Zuñiga-Lema
1
, Mario Paguay-Cuvi
1
, Arquímides Haro
1
, Antonio Meneses-Freire
2
1
Escuela Superior Politécnica Chimborazo,
2
Universidad Nacional de Chimborazo
lulyd13@hotmail.com
En este trabajo se desarrolla un método para calcular bandas de confianza con réplicas bootstrap,
usando modelos de regresión polinómicos ajustados a la variable medias de velocidad del viento
en cada hora-día de las estaciones, lluviosa y seca en la ciudad de Riobamba, Ecuador. Además
se compara la confiabilidad de las bandas de confianza bootstrap con las bandas asintóticas en
diseños de pares de puntos simulados.
Palabras claves: bandas bootstrap, regresión polinómica.
In this paper, a method is developed to calculate confidence bands with bootstrap replicates, using
polynomial regression models adjusted to variable wind speed averages in each hour-day of the
rainy and dry seasons in the city of Riobamba, Ecuador. We also compare the reliability of the
bootstrap confidence bands with the asymptotic bands in simulated point pair designs.
Keywords: bootstrap bands, polynomial regression.
INTRODUCCIÓN
Las bandas de confianza con ajustes de modelos de regre-
sión polinómicos son de importante utilidad para esta-
blecer la calidad de ajuste y estimación del modelo (5). El
problema para calcular estas bandas con el método están-
dar (bandas de confianza asintóticas) es la dependencia
de la naturaleza de los residuos del modelo ajustado (3,4)
(normalidad de los residuos y varianza residual constan-
te). En este trabajo se desarrolla y se aplica un método de
bandas bootsrap independiente de la normalidad de los
residuos del modelo (1,2), en acuerdo a lo siguiente:
Primero, se realiza un enfoque teórico de: modelo de
regresión polinómico de orden p, método de mínimos
cuadrados para la estimación de los parámetros, y de la
expresión de la desviación típica residual del modelo.
Segundo, se propone el algoritmo para calcular las ban-
das de confianza bootstrap con el modelo polinómico
ajustado.
Tercero, se realizan los resultados y las
discusiones de las aplicaciones de los
modelos de regresión polinómicos y sus
bandas de confianza bootstrap para la
variable medias de velocidad del vien-
to en cada hora-día de las estaciones,
lluviosa y seca. También se compara la
confiabilidad de las bandas de confianza
bootstrap con las bandas asintóticas en
diseños de pares de puntos simulados.
Por último se da las conclusiones del tra-
bajo.
MODELO DE
REGRESIÓN POLINÓMICO
Los modelos de regresión polinómicos
son una generalización de los modelos
de regresión lineal, y permiten descri-
bir el comportamiento en promedio de
la variable repuesta Y condicionada por
valores de una variable independiente X
R
esumen
A
bstract
ISSN 1390-5740 Número 17 Vol. 1 (2017)
ISSN 2477-9105
Fecha de recepción: 08/11/2017
Fecha de aceptación: 15/05/2017
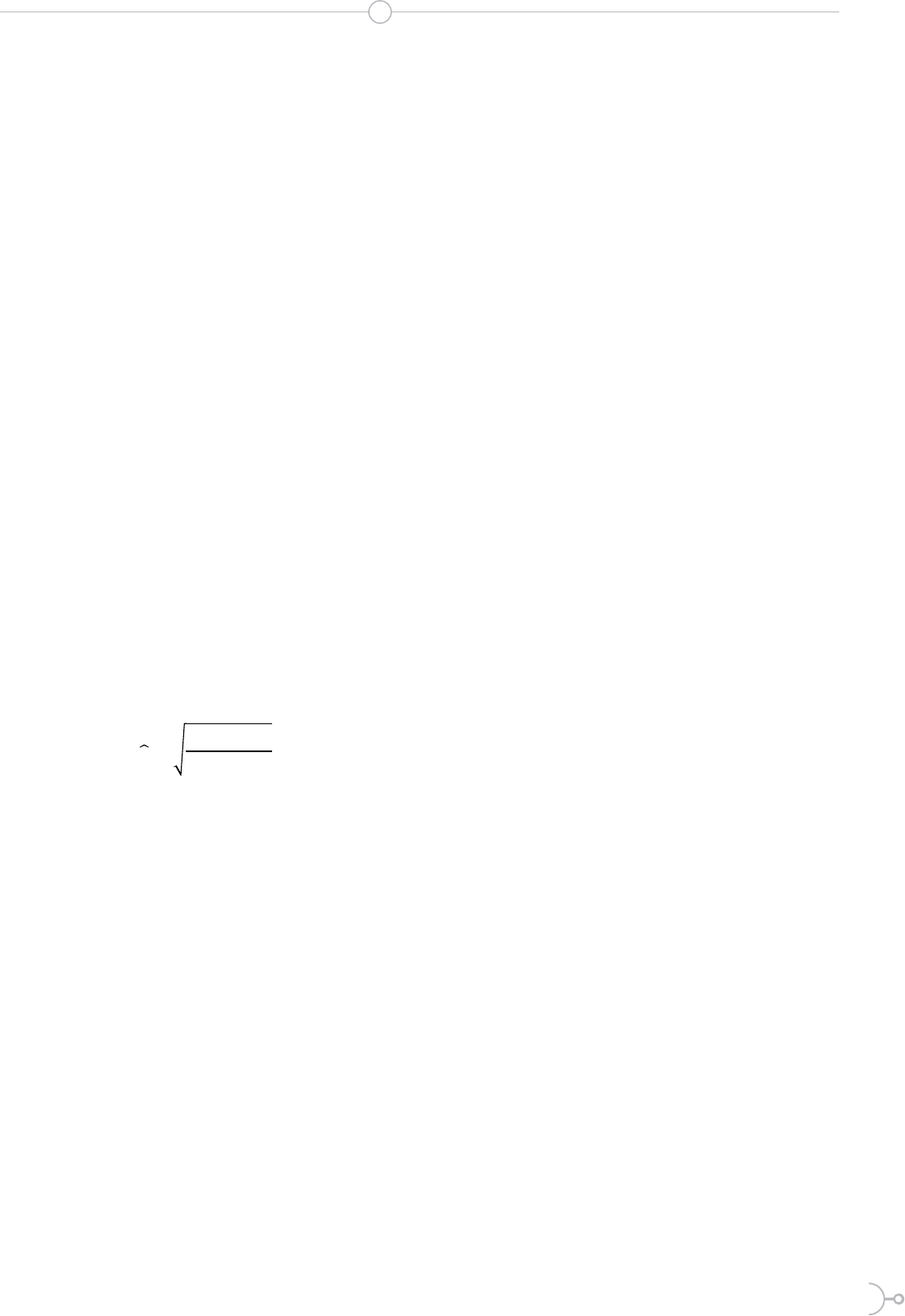
13
utilizando una representación funcional
polinomial (5):
Y = m(X) + ε (1)
o de forma ampliada la ecuación (1),
Y = a
0
+ a
1
X +
…
+ a
p
X
p
+ ε (2)
Los estimadores de los parámetros a
0
,
a
1
, … a
p
, definen el polinomio de regre-
sión de orden p, y se calculan con el mé-
todo de mínimos cuadrados. Esto es, a
partir de una muestra (X
1
, Y
1
),(X
2
,Y
2
),
… (X
n
,Y
n
), las estimaciones â
0
,â
1
, … ,
â
p
se obtienen minimizando la siguiente
suma de residuos al cuadrado:
(Y
1
- Ŷ
1
)
2
+
… + (Y
n
- Ŷ
n
)
2
(3)
donde, Ŷ
i
=
a
0
+ a
1
X
1
+
… + a
p
X
i
p
Con respecto al error aleatorio ε supo-
ne que sigue la distribución gaussiana,
ε ~ N(0,σ
2
) con media nula y varianza
poblacional σ
2
. Como estimador de σ, se
utiliza la desviación típica residual dada
por:
(4)
donde e
i
2
= (Y
1
- Ŷ
1
)
2
Bandas de confianza asintóticas con
modelos de regresión polinómicos
La estimación de Y
i
puede no ser sufi-
ciente para determinar el efecto de X
i
.
En ocasiones, para cada punto x interesa
conocer el intervalo donde se sitúa el hi-
potético valor Y
i
(x) con una determinada
probabilidad (3,4). Para la construcción
de dicho intervalo, es necesario conocer
las estimaciones Ŷ
i
mediante un ajuste
polinómico, la función lm del software
estadístico R (8) permite calcular este
ajuste y la estimación de la desviación tí-
pica residual σ̂ de las estimaciones Ŷ
i
.
Por tanto el intervalo de confianza asin-
tótico de cada estimación Ŷ
i
con nivel de
confianza 1 – α viene dado (3,4):
Ŷ
i
± z
1 – α/2
*σ̂ (5)
siendo z
1 – α/2
el cuantil de orden 1 – α/2 de la distribución
normal estandarizada. Todos estos intervalos forman las
bandas de confianza asintóticas con nivel de confianza
1 – α.
Nótese que para calcular estas bandas de confianza el
error aleatorio ε supone que sigue la distribución nor-
mal, ε ~ N(0,σ
2
) con media nula y varianza poblacional
σ
2
constante.
BANDAS DE CONFIANZA BOOTSTRAP CON MO-
DELOS DE REGRESIÓN POLINÓMICOS
Los intervalos de confianza bootstrap en cada ordenada
estimada Ŷ
i
mediante el modelo de regresión polinómico,
forman las bandas de confianza bootstrap calculadas con
el siguiente algoritmo:
1. Calcular los parámetros â
0
, â
1
,… , â
p
y σ̂ del modelo
de regresión polinómico.
2. Generar un número B de muestras bootstrap que imi-
tan la muestra original de acuerdo a lo siguiente: Del
modelo de regresión polinómico estimado,
Ŷ = m̂ (X) + ε̂ (6)
donde ε̂ ~ N(0,σ̂ 2 ), se simula ε* de forma aleato-
ria con la distribución normal N(0, σ̂ 2), obteniendo
muestras bootstrap {(X
1
,Y
1
*),(X
2
, Y
2
*),…,(X
n
, Y
n
*)}
(i)
con i = 1, 2, … , B, donde
Y* = m̂ (X) + ε*
3. Con cada una de las muestras bootstrap se realiza un
ajuste polinómico, obteniendo al final B ajustes.
4. Para cada valor de X, el intervalo de confianza boots-
trap de Ŷ es calculado con los siguientes pasos:
• Las B estimaciones bootstrap, Ŷ*
(1)
, … , Ŷ*
(B)
ordenar
de forma creciente en cada X, Ŷ*
(b)
, b = 1,…,B.
• Las curvas formadas por los cuantiles q/2 y 1 - q/2 de
Ŷ
j
*
(b)
, b=1,…,B en cada X
j
con j = 1, … , n, son los lí-
mites inferior y superior de las bandas de confianza
bootstrap de Ŷ.
Zuñiga, Paguay, Haro, Meneses
14
RESULTADOS Y DISCUSIÓN
El desarrollo del trabajo se realiza con velocidades del
viento (medida en metro por segundo m/s), tomadas en
la Estación Meteorológica de la Facultad de Ciencias de la
Escuela Superior Politécnica de Chimborazo en la ciudad
de Riobamba, Ecuador. Estas velocidades se generan a 20
metros del suelo y son registradas cada 10 minutos, empe-
zando a las 0 horas hasta las 23 horas 50 minutos de cada
día durante los 365 días del año 2009.
Estos datos se convierten en formato texto mediante el
software Symphonie Data Retriever (software de la Esta-
ción), formando una matriz de 365 filas con 144 columnas.
Dos bases de datos de las velocidades del viento son usadas,
la primera de medias de velocidades por cada hora de la
estación lluviosa dada en los meses: enero, febrero, marzo,
abril, mayo, octubre, noviembre, diciembre, y la segunda
de medias de velocidades por cada hora de la estación seca
dada en los meses: junio, julio, agosto y septiembre (web
oficial del INAMHI: http://www.serviciometeorologico.
gob.ec/cambio-climatico/ ).
Ajustes de modelos de regresión polinómicos para me-
dias de velocidades del viento en cada hora-día.
Los polinomio de regresión ajustados para las medias de
velocidades del viento en los meses de estación lluviosa y
seca son de orden 7:
Y= a
0
+ a
1
X +…+ a
7
X
7
+ ε, (7)
donde los parámetros estimados de este polinomio, â
0
, â
1
, …
, â
p
y σ̂ se calculan usando las librerías del software R (8).
Tabla 1. Resumen del modelo de regresión polinómico
ajustado (estación lluviosa)
En la Tabla 1, se observa que los coefi-
cientes estimados del modelo son signi-
ficativos con niveles de confianza mayo-
res al 99%, al igual que la significación
del modelo en su totalidad. También este
modelo tiene la variación explicada ma-
yor al 99% según el R2 ajustado (Tabla
2). Los dos modelos ajustados son esta-
dísticamente muy buenos para explicar
las variaciones de los promedios de ve-
locidades del viento en cada hora de las
dos estaciones (tablas 1 y 2).
Tabla 2. Resumen del modelo de regresión
polinómico ajustado (estación seca).
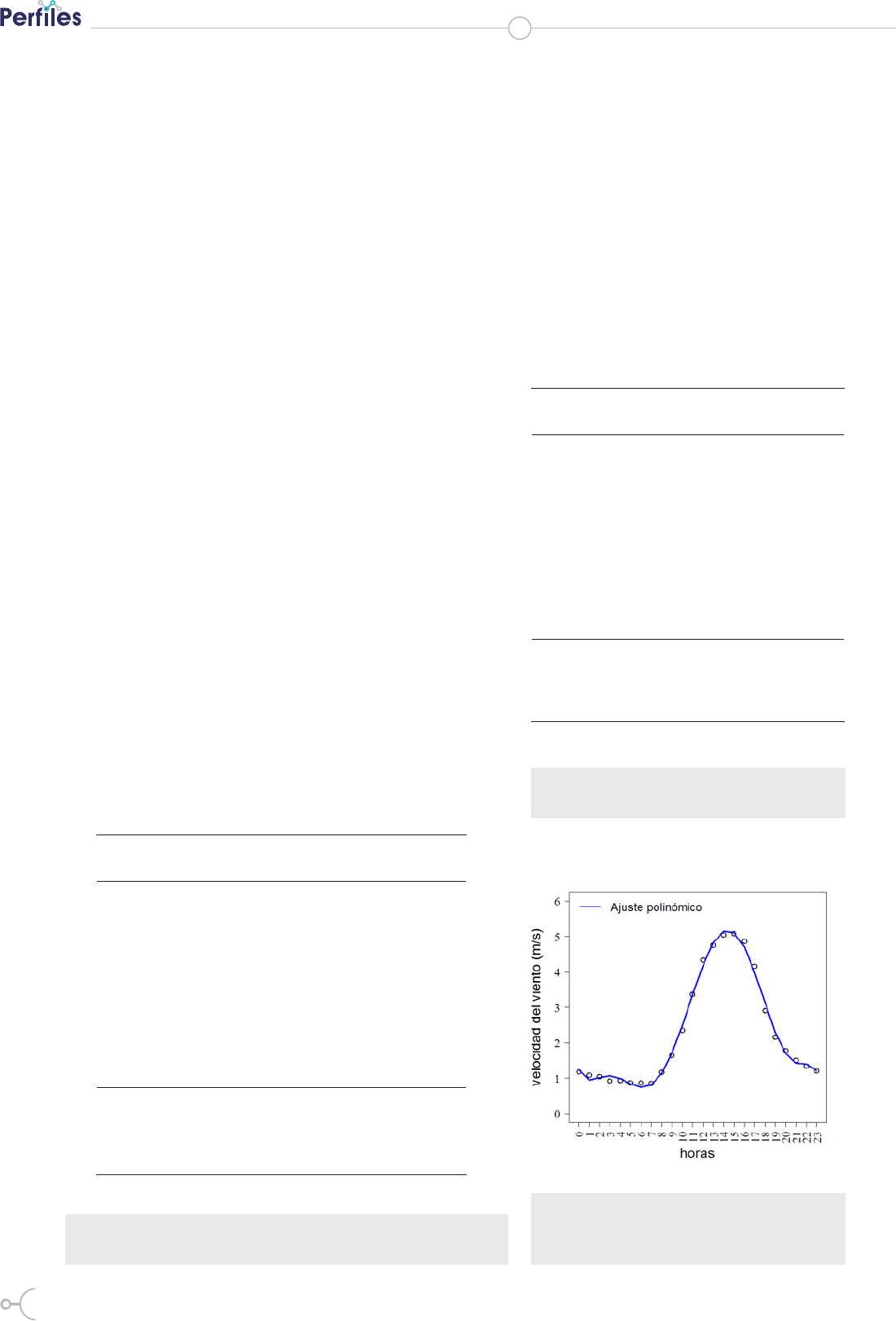
Figura 1. Medias de velocidades del viento
en cada hora y modelo polinómico de
orden 7 ajustado (estación lluviosa).
Coecient. Valor estimado Probabilidad
de rechazo
â
0
1.246e+00 < 0.01
â
1
-7.205e-01 < 0.01
â
2
5.865e-01 < 0.01
â
3
-1.893e-01 < 0.01
â
4
2.773e-02 < 0.01
â
5
-1.945e-03 < 0.01
â
6
6.436e-05 < 0.01
â
7
-8.108e-07 < 0.01
Error estándar residual σ̂ 0.1297
R
2
ajustado 99.31%
Probabilidad de rechazo
del modelo polinómico < 0.01
Coecient. Valor
estimado
Probabilidad
de rechazo
â
0
1.373e+00 < 0.01
â
1
-5.155e-01 < 0.1
â
2
4.467e-01 < 0.01
â
3
-1.592e-01 < 0.01
â
4
2.502e-02 < 0.01
â
5
-1.824e-03 < 0.01
â
6
6.166e-05 < 0.01
â
7
-7.859e-07 < 0.01
Error estándar residual σ 0.1441
R
2
ajustado 99.47%
Probabilidad de rechazo
del modelo polinómico < 0.01
ISSN 1390-5740 Número 17 Vol. 1 (2017)
ISSN 2477-9105

15
Figura 2. Medias de velocidades del viento
en cada hora y modelo polinómico de
orden 7 ajustado (estación seca).
En las figuras 1 y 2 se observa que los
promedios o medias de velocidades del
viento a las 15 horas y sus entornos cer-
canos, son mayores en la estación seca
que en la estación lluviosa.
Bandas de confianza bootstrap de las
medias de velocidades del viento en
cada hora del día.
Las réplicas bootstrap realizadas con los
modelos polinómicos ajustados para las
medias de las velocidades del viento ha-
cen posible calcular las bandas de con-
fianza bootstrap al 95% y 99% en las
estaciones, lluviosa y seca.
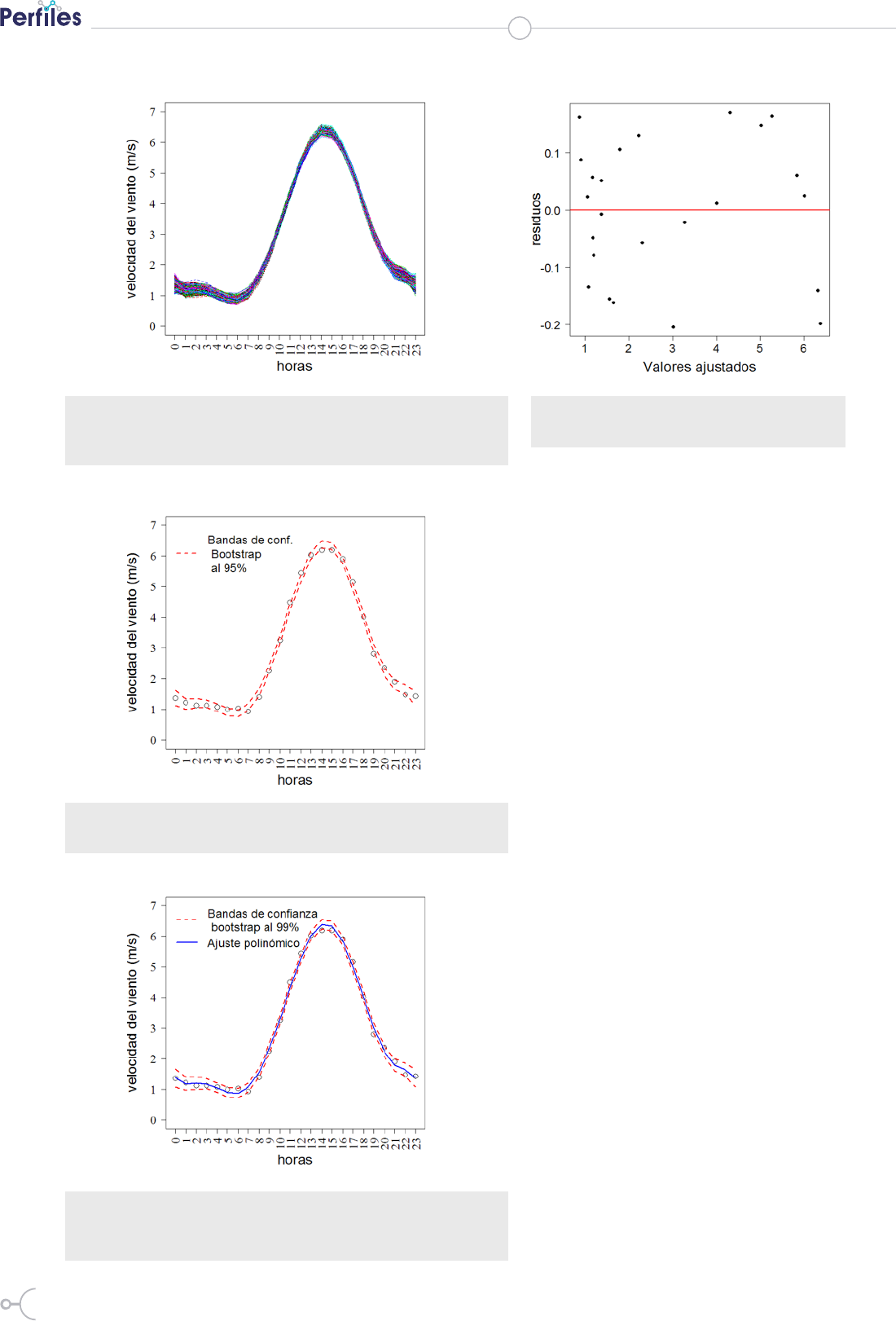
Figura 3. Mil réplicas bootstrap de modelos
polinómicos ajustados de medias de
velocidades del viento en cada hora-día
(estación lluviosa).
Figura 4. Velocidades del viento versus horas, y bandas de
confianza bootstrap al 95% (estación lluviosa).
Figura 5. Velocidades del viento versus horas, bandas de
confianza bootstrap al 99% y polinomio ajustado de orden 7
(estación lluviosa).
Figura 6. Aleatoriedad de residuos del modelo polinómico
de orden 7 (estación lluviosa).
Zuñiga, Paguay, Haro, Meneses
16
Figura 7. Mil réplicas bootstrap de modelos polinómicos
ajustados de medias de velocidades del viento en cada
hora-día (estación seca).
Figura 8. Velocidades del viento versus horas, y bandas de
confianza bootstrap al 95% (estación seca).
Figura 9. Velocidades del viento versus horas, bandas de
confianza bootstrap al 99% y polinomio ajustado de orden 7
(estación seca).
Figura 10. Aleatoriedad de residuos del mo-
delo polinómico de orden 7 (estación seca).
En las figuras que contienen bandas de
confianza bootstrap se observan que
estas tienen anchos muy pequeños, no-
tando gráficamente que los ajustes de los
modelos de regresión polinómicos son
óptimos. Los residuos de los dos mode-
los antes ajustados tienen media cero y
de varianza aproximadamente constan-
te (Figuras 6 y 10). Todos los resultados
son calculados con el software estadísti-
co R (8).
Comparación de las bandas
de confianza bootstrap con las
asintóticas
Se consideran dos diseños: el primero de
puntos simulados con un polinomio cú-
bico ligeramente perturbado con valores
de una distribución normal estándar
donde se estiman las bandas de confian-
za bootstrap y asintóticas, y el segundo
de puntos con un polinomio cúbico lige-
ramente perturbado con valores de una
distribución chicuadrado con 3 grados
de libertad donde únicamente se puede
estimar las bandas de confianza boots-
trap.
Primer diseño:
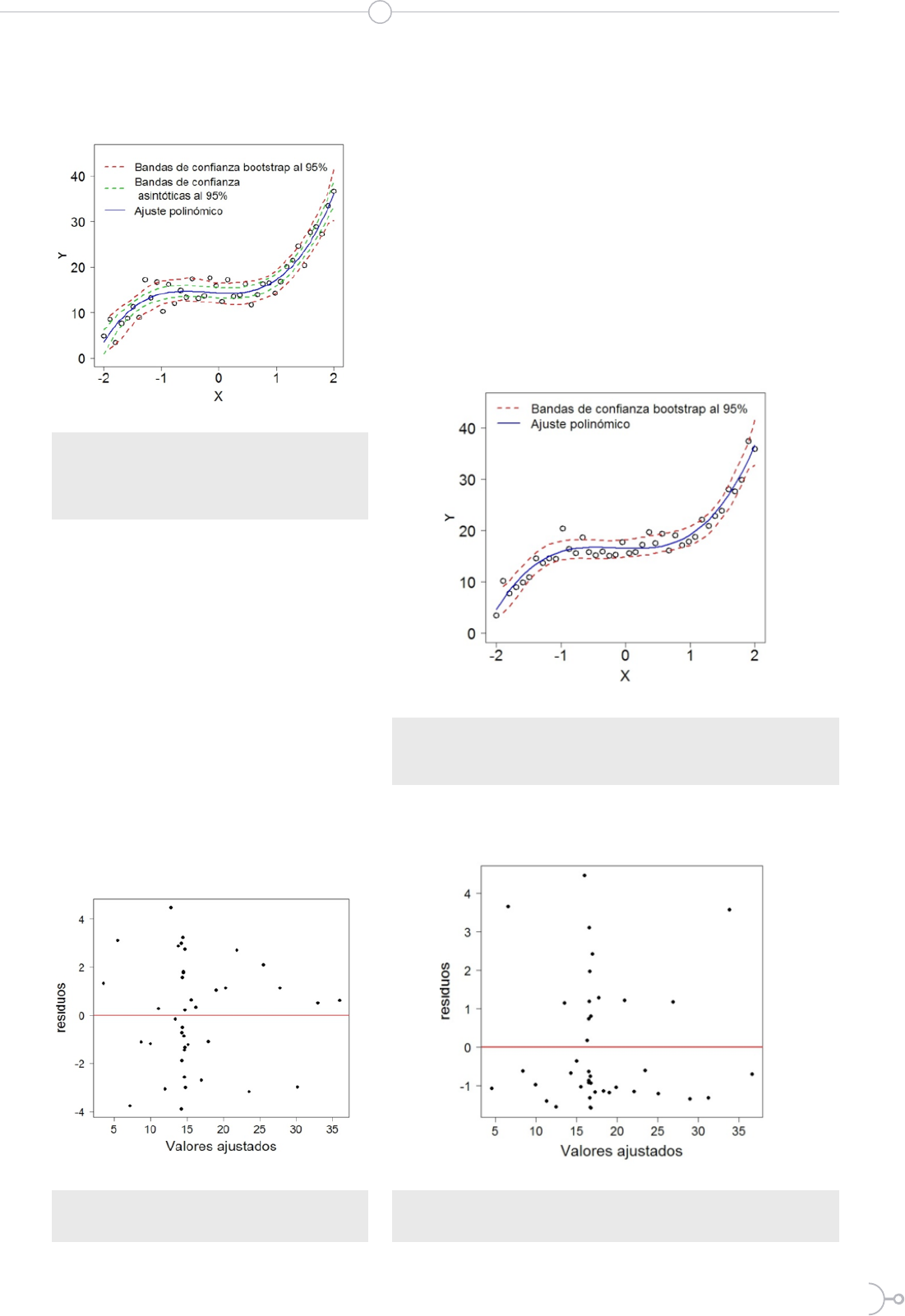
En la Figura 11 se observa la confiabili-
dad para estimar las bandas de confian-
ISSN 1390-5740 Número 17 Vol. 1 (2017)
ISSN 2477-9105
17
za bootstrap al ser más anchas que las
bandas asintóticas.
Figura 11. Puntos simulados con polinomio
cúbico más perturbación normal
estándar, bandas de confianza al 95% y
ajuste polinómico.
Las bandas de confianza asintóticas son
posibles calcular debido que los residuos
del polinomio ajustado se distribuyen
normalmente con un p-valor = 0.4127
de acuerdo al test de Shapiro-Wilk [6,7],
y también suponiendo que la varianza
residual del polinomio ajustado es cons-
tante (Figura 12).
Nótese que el cálculo de las bandas
bootstrap no requiere de la normalidad
y varianza constante de los residuos.
Figura 12. Aleatoriedad de residuos del
modelo polinómico de orden 3.
Segundo diseño:
En la Figura 13 se observa las bandas de confianza boots-
trap al 95%, los puntos simulados y el polinomio ajus-
tado mediante la función lm del software estadístico R
[8]. Los residuos del polinomio ajustado no se distribuyen
normalmente con un p-valor < 0.01 según el test de Sha-
piro-Wilk [6,7], además se observa en la Figura 14 que
los residuos no tienen varianza constante por tanto no es
posible calcular las bandas de confianza asintóticas. Esto
prueba que el método para calcular las bandas de con-
fianza bootstrap es más flexible.
Figura 13. Puntos simulados con polinomio cúbico más
perturbación chicuadrado, bandas de confianza bootstrap
al 95% y ajuste polinómico.
Figura 14. Aleatoriedad de residuos del modelo
polinómico de orden 3.
Zuñiga, Paguay, Haro, Meneses

R
eferencias
18
CONCLUSIONES
• El método bootstrap para calcular las bandas de con-
fianza, es una alternativa eficiente para determinar
los intervalos de confianza en cada valor ajustado del
polinomio de regresión.
• La fortaleza del método bootstrap para determinar
las bandas de confianza, es la aplicación con ajustes
de modelos polinómicos en condiciones residuales
obviando la normalidad, a diferencia de los métodos
tradicionales que dependen de la naturaleza residual
del modelo.
AGRADECIMIENTOS
A los directivos de la Estación Meteo-
rológica de la Facultad de Ciencias de la
Escuela Superior Politécnica de Chim-
borazo.
A la SENESCYT.
1. Davison, A.C. and Hinkley, D.V. Bootstrap Methods and their Application. Cambridge Univer-
sity Press; 1997.
2. Efron, B. and Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and
other measures of statistical accuracy. Statistical Science 1; 1986.
3. Gu. RKPACK and its application: Fitting smoothing spline models, Proc. Statistical Computing
Section, Amer. Statist. Assoc., pp. 42-51; 1998.
4. Hastie, T.J., Tibshirani, R.J. Generalized Additive Models. Chapman & Hall; 1990.
5. Johnson, R. Probabilidad y estadística para ingenieros. Vol 1. 8a ed. México: Pearson educación;
2012.
6. Patrick, R. An extension of Shapiro and Wilk's W test for normality to large samples. Applied
Statistics, 31, 115–124; 1982.
7. Patrick, R. Algorithm AS 181: The W test for Normality. Applied Statistics, 31, 176–180; 1982.
8. Rizzo, M.L. Statistical Computing with R. Chapman&Hall/CRC. 1a ed; 2008.
ISSN 1390-5740 Número 17 Vol. 1 (2017)
ISSN 2477-9105