
R
esumen
A
bstract
67
Meneses, Zuñiga, Haro
MÉTODO BOOTSTRAP PROPUESTO PARA HIPÓTESIS
CONCERNIENTES A LA DIFERENCIA DE MEDIAS EN VARIABLES
INDEPENDIENTES.
Antonio Meneses-Freire
1
, Lourdes Zuñiga-Lema
2
, Arquimides Haro
2
1
Universidad Nacional de Chimborazo
2
Escuela Superior Politécnica de Chimborazo
ameneses@unach.edu.ec
En este trabajo se propuso un método para calcular un intervalo de confianza con réplicas boots-
trap para la diferencia de medias de dos muestras independientes en el ámbito de la teoría de
hipótesis. La hipótesis nula se rechaza si el intervalo de confianza no contiene el 0, caso contrario
se acepta. Se comparó el método Paramétrico que usa la Z normal estándar y la t de la distribu-
ción t-Student con el método Bootstrap propuesto en diseños de muestras de tamaños grandes,
pequeñas e independientes, con suposiciones fuertes para el método Paramétrico, haciendo notar
que estas suposiciones no son necesarias para el método Bootstrap. También se realizó una apli-
cación del método propuesto con la variable meteorológica promedios de radiación solar en cada
hora-día, para probar la diferencia en medias de radiación en las épocas lluviosa y seca en la ciudad
de Riobamba, Ecuador.
Palabras claves: método bootstrap, diferencia de medias.
In this paper we propose a method to calculate a confidence interval with bootstrap replicates for
the mean difference of two independent samples in the field of hypothesis theory. The null hypo-
thesis is rejected if the confidence interval does not contain 0, otherwise it is accepted. We compare
the parametric method using the standard normal Z and the t-Student t distribution with the pro-
posed Bootstrap method in large, small, independent sample designs with strong assumptions for
the parametric method, noting that these assumptions Are not required for the Bootstrap method.
An application of the proposed method with the meteorological variable averages of solar radiation
every hour-day is also carried out to test the difference in radiation averages in the rainy and dry
seasons in the city of Riobamba, Ecuador.
Key words: bootstrap method, mean difference.
INTRODUCCIÓN
El método Paramétrico común para
diferencia de medias en el contexto de
la teoría de hipótesis tiene condicio-
nes o suposiciones fuertes que deben
cumplir las muestras, una de ellas es
la normalidad (3,8). El método Boots-
trap que se propuso es muy flexible en cuanto a que
las variables sean normales o no. Este método Boots-
trap principalmente se centró en calcular un interva-
lo de confianza para la diferencia de medias de dos
muestras independientes en acuerdo a lo siguiente:
Se comparó dos tratamientos de datos usando el mé-
todo Paramétrico frente al método Bootstrap pro-
Fecha de recepción: 09-12-2016
Fecha de aceptación:15-05-2017

68
puesto en diseños de dos muestras independientes
con suposiciones fuertes (una de ellas la normalidad),
para poder aplicar el estadístico Z normalizado y el t
de la t-Student del método Paramétrico en muestras
grandes y pequeñas respectivamente, haciendo notar
que para el método Bootstrap estas suposiciones no
son necesarias (3,4).
Se obtuvieron resultados del método Paramétrico
aplicado en diseño de variables limitadas por suposi-
ciones (una de ellas es la normalidad), y la ampliación
de estos diseños en los que también el método Boots-
trap es aplicable (1,2). Para complementar esta am-
pliación se obtuvieron los resultados de la aplicación
del método Bootstrap en muestras correspondientes
a radiación solar en las épocas lluviosa y seca en la
Ciudad de Riobamba, Ecuador.
COMPARACIÓN DE DOS TRATAMIENTOS DE
DATOS USANDO METODOS PARAMÉTRICO Y
BOOTSTRAP (PROPUESTO)
En la ciencia ocurren avances cuando las nuevas ideas
conducen a mejorar o ampliar el campo de aplicación de
metodologías existentes. Cualquier procedimiento nuevo
debe compararse con los existentes y la cantidad de mejo-
ramientos valorado (3).
En los siguientes apartados se estudian el diseño de
muestras independientes (existe entre sus elementos alea-
toriedad completa), la comparación de dos muestras con
el método Paramétrico elemental con sus respectivas su-
posiciones para poder usar la variable Z normal estanda-
rizada en muestras grandes (mayores o iguales a 30) y la t
de la distribución t-Student para muestras pequeñas (me-
nores que 30). Junto a este método Paramétrico se aplicó
el método Bootstrap propuesto.
Método paramétrico para diferencia de medias en
muestras grandes independientes
Suposiciones: muestras grandes (3,9)
• X= {X
1
, X
2
, … ,X
n
} es una muestra aleatoria de tamaño
n de la población 1, que tiene media μ
1
y varianza σ
2
1
.
• Y= {Y
1
, Y
2
, … ,Y
m
} es una muestra aleatoria de tamaño
m de la población 2, que tiene media μ
2
y varianza σ
2
2
.
• Las dos muestras X
1
,X
2
,…,X
n
y Y
1
,Y
2
,…,Y
m
son inde-
pendientes con medias , X̅ , Ȳ y va-
rianzas S
2
X
, S
2
Y
respectivamente.
Pruebas de muestras grandes para di-
ferencias de medias:
Al formular el problema de forma gene-
ral, se deben considerar dos poblaciones
con medias μ
1
y μ
2
así como las varian-
zas σ
2
1
, y σ
2
2
. Se quiere probar la hipóte-
sis nula
H
0
: μ
1
- μ
2
= δ
0
(1)
donde δ
0
es una constante especificada,
sobre la base de muestras aleatorias in-
dependientes de tamaños n y m. Cuando
los tamaños de muestra son grandes, el
teorema central del límite implica que
X̅ y Ȳ son aproximadamente normales
(8), además por la independencia su di-
ferencia también es aproximadamente
normal y
Var (2)
Con las suposiciones a, b, c y la ecuación
2 se obtiene el estadístico Z definido:
(3)
que es aproximadamente normal están-
dar a pesar de sustituir las varianzas σ
2
1
y σ
2
2
de las poblaciones con las varianzas
S
2
X
y S
2
Y
de las muestras (3,8).
Tabla 1: Regiones críticas para probar
μ1 - μ2=δ0 en poblaciones normales con
σ1 y σ2 conocidas o en muestras grandes
n,m ≥30 (3).
Hipótesis
alternativa
Rechazar hipótesis
nula si:
"
−
%
<
(
Z < −z
+
"
−
%
>
(
Z > z
+
"
−
%
≠
(
Z < −z
+
obienZ > −z
+
X − Y
=
%
&
'
(
+
%
'
'
*
Z =
X − Y −
0
S
X
2
+
S
Y
2
ISSN 1390-5740 Número 17 Vol. 1 (2017)
ISSN 2477-9105
69
En la Tabla 1, δ
0
puede ser cualquier
constante, pero en la gran mayoría
de las aplicaciones su valor es cero y
z
α
es el cuantil de la normal estándar
(normal con media 0 y desviación típica
1, N(0,1)).
Aplicación de diferencia de medias en
muestras grandes:
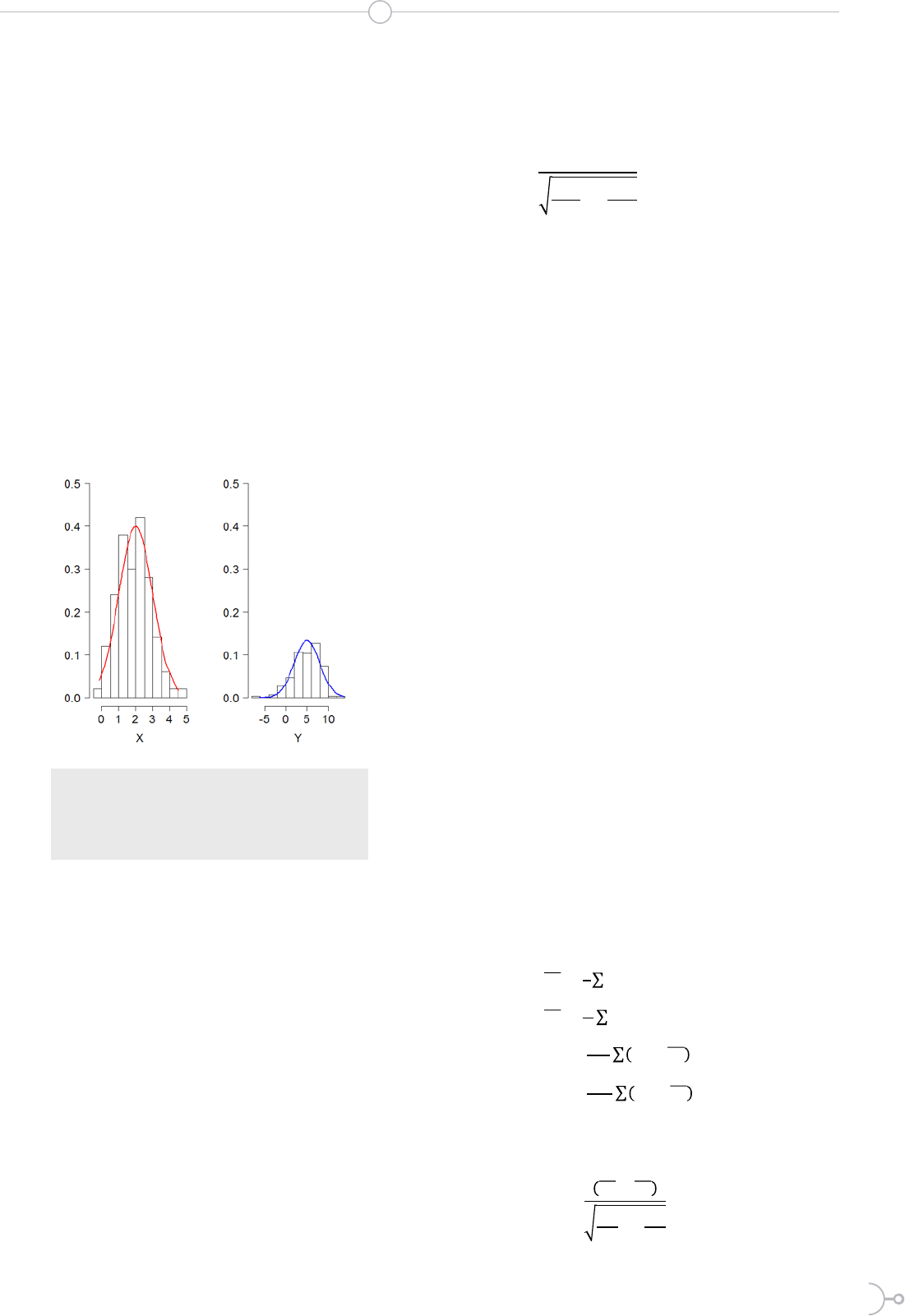
En la Figura 1 se observan dos muestras
grandes que se distribuyen normalmen-
te, X con media 2 y desviación típica 1 e
Y con media 5 y desviación típica 3, es
decir:
X ~ N(2 , 1) e Y ~ N(5 , 3) (4)
Figura 1: X e Y muestras aproximadamente
normales de tamaños 100 y 150 respecti-
vamente, simuladas mediante la función
rnorm del software estadístico R (6).
Estas dos muestras cumplen los supues-
tos a, b y c para aplicar el método Pa-
ramétrico con el estadístico Z normali-
zado.
La prueba se realizó en 5 pasos que se
usan en teoría de hipótesis (3,8):
1. Hipótesis
H
0
: μ
1
- μ
2
=0
H
1
: μ
1
- μ
2
≠0
2. Nivel de significancia α = 0.05
3. Criterio: rechazar la hipótesis nula si
z > 1.96 o z < -1.96, donde z es el
estadístico definido en la ecuación 3 y z
0.975
= 1.96.
4. Cálculo del valor del estadístico:
5. Decisión: puesto que z < z
0.975
, H
0
es rechazada (ver
Tabla 1), es decir la diferencia observada entre las dos
medias muestrales es significativa al 95 % de con-
fianza.
Método propuesto Bootstrap para la diferencia de me-
dias en muestras grandes independientes
El método Bootstrap es un procedimiento estadístico
que sirve para aproximar la distribución en el muestreo
normalmente de un estadístico (2). Para ello se proce-
de mediante remuestreo, es decir, obteniendo muestras
mediante algún procedimiento aleatorio que utilice la
muestra original. Su ventaja principal es que no requiere
supuestos sobre el mecanismo generador de los datos (1).
En base a los aspectos generales de este método se calculó
el intervalo de confianza para la diferencia de medias de
dos muestras usando los siguientes pasos:
1. Dadas dos muestras independientes de tamaños n y m.
X = {X
1
, X
2
, … ,X
n
}
Y = {Y
1
, Y
2
, … ,Y
m
}
crear la muestra ampliada:
A= {X
1
, X
1
, … ,X
n
, Y
1
, Y
2
, … ,Y
m
}
y luego mezclar sus elementos.
2. Para cada i = 1,2, … , n arrojar
U
i
~U(0,1) y hacer X
i
*
= A
[nUi ]+1
3. Para cada i = 1,2, … , m arrojar
U
i
~U(0,1) y hacer Y
i
*
= A
[mUi]+1
4. Obtener:
5. Calcular el estadístico bootstrap:
Meneses, Zuñiga, Haro
z =
2 − 5
1
(
100
+
3
(
150
= −11.34
• X
∗
=
$
%
X
&
∗
• Y
∗
=
$
(
Y
&
∗
• S
*
∗
+
=
$
%,$
X
&
∗
− X
∗
+
• S
.
∗
+
=
$
(,$
Y
&
∗
− Y
∗
+
R
∗
=
X
∗
− Y
∗
S
)
∗
*
+
S
-
∗
*

70
6. Repetir B veces los pasos 2-5 para obtener las réplicas
bootstrap R*
(1)
, … , R*
(B)
del estadístico R* que se dis-
tribuye con N(0,1) para valores de B grandes (teorema
central del límite (3))
7. Ordenar de forma creciente los valores del estadístico
bootstrap del paso 6:
R*
(b)
, b = 1, 2, … , B
8. Calcular los puntos críticos, inferior y superior del ni-
vel de significancia α:
p.c.inf =
p.c.sup =
donde [ x ] es la función parte entera de x, U(0,1) es la
distribución uniforme en el intervalo (0,1).
9. Calcular los límites inferior y superior del intervalo de
confianza para hipótesis concernientes a la diferencia
de medias poblacionales μ
1
- μ
2
con el nivel de signifi-
cancia α.
despejando μ
X
- μ
Y
se tiene:
lim.inf = (X̅ - Ȳ) - p.c.sup
lim.sup = (X̅ - Ȳ) - p.c.inf
Aplicación del método Bootstrap a la diferencia de
medias en muestras grandes:
X e Y son muestras grandes usadas en el método Paramé-
trico.
1. Hipótesis,
H
0
: μ
1
- μ
2
= 0
H
1
: μ
1
- μ
2
≠ 0
2. Nivel de significancia α = 0.05
3. Criterio: aceptar H
0
cuando el 0 pertenece al intervalo
de confianza del método Bootstrap, caso contrario H
0
es rechazada.
4. El intervalo de confianza Bootstrap al 95% se calcu-
ló siguiendo los pasos del algoritmo del
método Bootstrap propuesto con 1000
réplicas para que el estadístico R* se dis-
tribuya aproximadamente a la normal
estándar N(0,1).
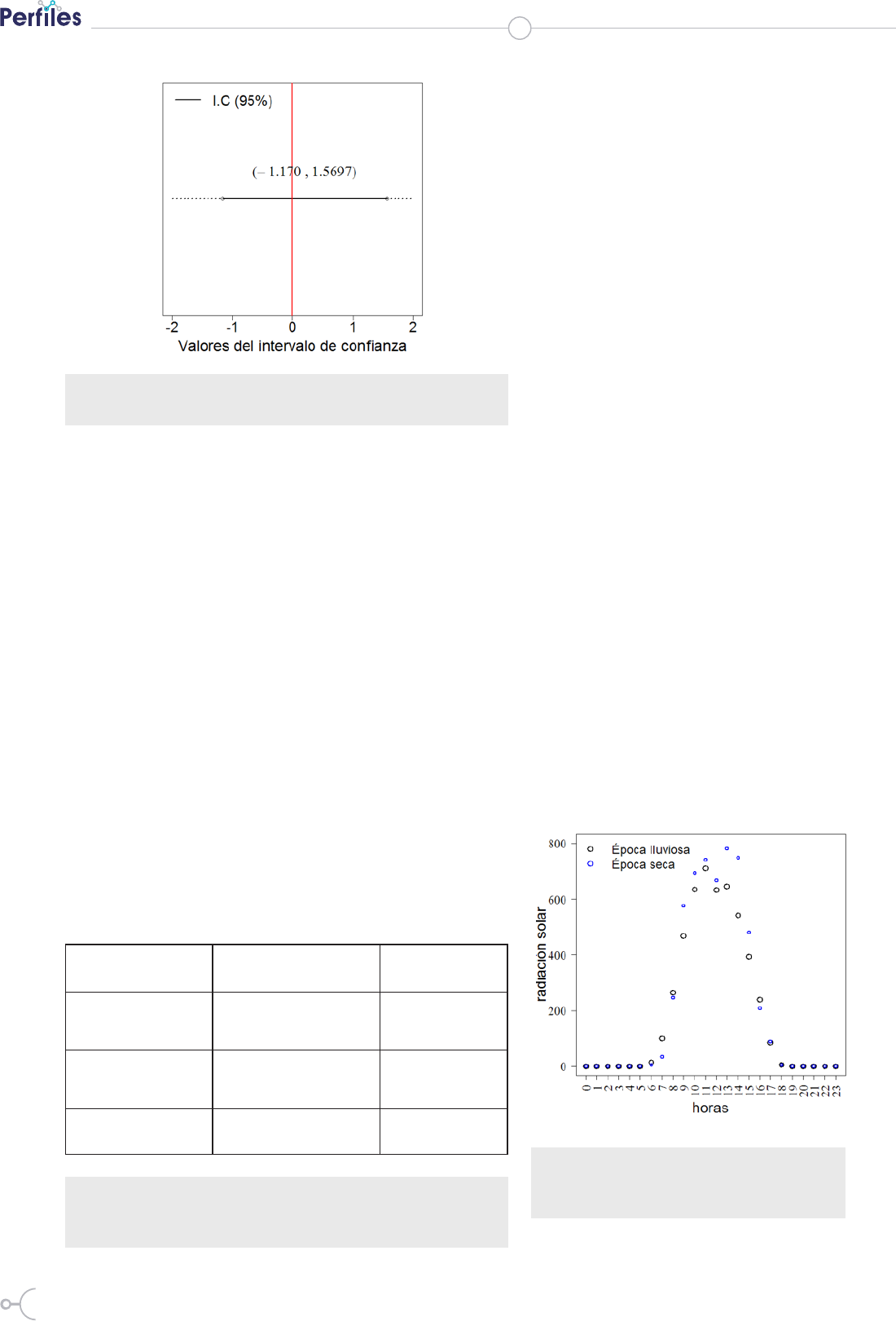
Figura 2: Intervalo de confianza Bootstrap
al 95 % para la diferencia de medias de las
muestras X e Y.
5. Decisión: en la Figura 2 se observa
que el intervalo de confianza.
Bootstrap no contiene el 0, H0 se recha-
za, es decir que las medias de las mues-
tras X e Y no son significativamente
iguales al 95 % de confianza.
Los resultados de este método Bootstrap
propuesto coinciden con el método Pa-
ramétrico. Pero nótese que el método
Bootstrap no necesita las suposiciones
fuertes del método Paramétrico.
Método Paramétrico para diferencia
de medias en muestras pequeñas inde-
pendientes.
Suposiciones adicionales para mues-
tras pequeñas:
• Ambas poblaciones deben ser nor-
males de las que se obtienen las mues-
tras.
• Las dos desviaciones típicas poblacio-
nales deben ser iguales σ
1
= σ
2
= σ.
Con todas las suposiciones a, b, c, d y e,
S
"
#
+
S
'
#
S
"
#
+
S
'
#
ISSN 1390-5740 Número 17 Vol. 1 (2017)
ISSN 2477-9105
71
la varianza de X̅ - Ȳ se convierte en
(5)
Se estima σ
2
mediante el estimador com-
binado (3):
(6)
El estadístico para prueba de muestras
pequeñas concernientes a la diferencia
entre dos medias con σ
1
y σ
2
desconoci-
das pero iguales viene dado:
(7)
y se distribuye mediante una t-Student
con n + m - 2 grados de libertad, S
p
se
obtiene de la ecuación 6. Las regiones de
rechazo de H
0
para t son análogas a las
de la Tabla 1.
Aplicación de diferencia de medias
para muestras pequeñas:
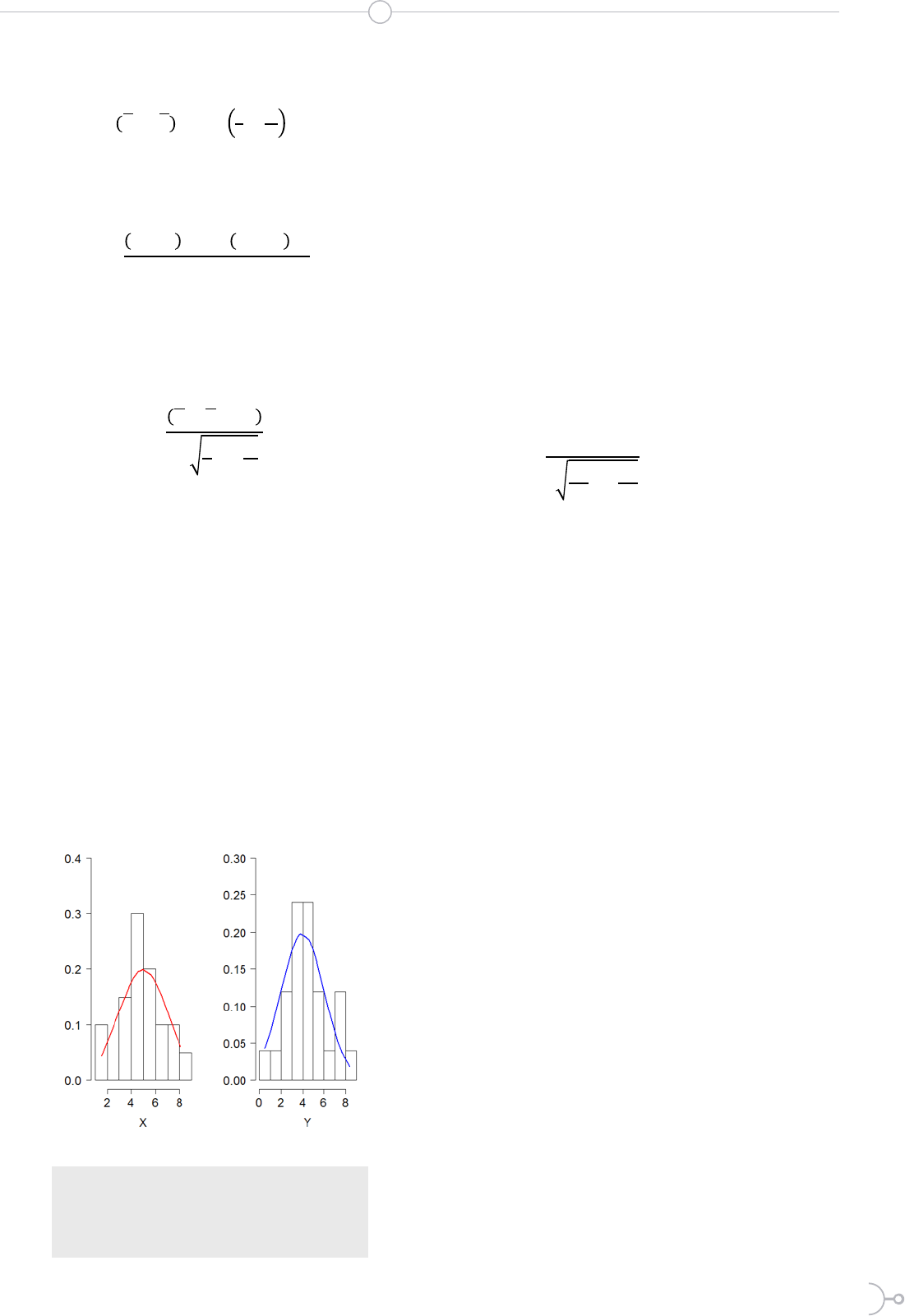
En la Figura 3 se observan dos muestras
pequeñas que se distribuyen normal-
mente:
X ~ N(5 , 2) e Y ~ N(4, 2) (8)
Figura 3.- X e Y muestras pequeñas apro-
ximadamente normales de tamaños 12 y
15 respectivamente, simuladas mediante la
función rnorm del software estadístico R (6).
Estas dos muestras cumplen los supuestos a, b, c, d y e
para aplicar el método Paramétrico con el estadístico t de
la distribución t-Student.
1. Hipótesis,
H
0
: μ
1
- μ
2
= 0
H
1
: μ
1
- μ
2
≠ 0
2. Nivel de significancia α = 0.05
3. Criterio: rechazar H
0
si t > 2.06 o t < - 2.06, donde t
es el estadístico definido en la ecuación 7 y 2.06 es el
valor del cuantil de la t-Student t (0.975 , 25).
4. Cálculo del valor del estadístico:
5. Decisión: puesto que t = 1.29 esta entre -2.06 y 2.06,
H0 no es rechazada es decir la diferencia observada
entre las dos medias muestrales no es significativa al
95 % de confianza.
Método propuesto Bootstrap para la diferencia de me-
dias en muestras pequeñas independientes
X e Y son muestras pequeñas usadas en la aplicación del
método Paramétrico.
1. Hipótesis,
H
0
: μ
1
- μ
2
= 0
H
1
: μ
1
- μ
2
≠ 0
2. Nivel de significancia α = 0.05
3. Criterio: aceptar H
0
cuando el 0 pertenece al interva-
lo de confianza Bootstrap, caso contrario la hipótesis
nula es rechazada.
4. El intervalo de confianza Bootstrap al 95 % se calculó
siguiendo los pasos del algoritmo del método Boots-
trap propuesto con 1000 réplicas para que el estadís-
tico bootstrap R* se distribuya aproximadamente a la
normal estándar N(0,1).
Meneses, Zuñiga, Haro
Var
S
"
#
=
− 1 S
)
#
+ − 1 S
,
#
+ − 2
=
X − Y −
(
S
*
1
+
1
=
5 − 4
2
1
12
+
1
15
= 1.29
72
Figura 4: Intervalo de confianza Bootstrap al 95% para la
diferencia de medias de las muestras X e Y.
5. Decisión: en la Figura 4 se observa que el intervalo de
confianza Bootstrap contiene el 0, H0 no se rechaza,
es decir que las medias de las variables X e Y son sig-
nificativamente iguales al 95% de confianza.
Los resultados de este método Bootstrap propuesto coin-
ciden con el método Paramétrico también para muestras
pequeñas. Pero nótese nuevamente que el método Boots-
trap no necesita las 5 suposiciones del método Paramé-
trico.
RESULTADOS Y DISCUSIÓN
Resultados de la sección 2:
En la Tabla 2 se observan los diseños de variables o mues-
tras limitados donde se aplicó el método Paramétrico de
acuerdo a las suposiciones a, b, c, d, y e de la sección 2,
además los resultados del método Bootstrap en estos di-
seños de muestras independientes.
Tabla 2: Diseños de aplicación de los métodos
Paramétrico y Bootstrap en inferencias concernientes
a diferencia de medias.
Aplicación del método Bootstrap en
radiación solar:
Fuente de datos:
La aplicación práctica se realizó con la
variable meteorológica radiación solar
(medida en vatio por metro cuadrado
W.m
-2
), tomada en la Estación Meteo-
rológica de la Facultad de Ciencias de la
Escuela Superior Politécnica de Chim-
borazo en la ciudad de Riobamba, Ecua-
dor. Esta variable es registrada cada 10
minutos, empezando a las 0 horas hasta
las 23 horas 50 minutos de cada día du-
rante los 365 días del año 2009. Esta base
de datos se divide de acuerdo a dos épo-
cas lluviosa y seca. Época lluviosa en los
meses enero, febrero, marzo, abril, mayo,
octubre, noviembre, diciembre, y época
seca en los meses junio, julio, agosto y
septiembre (tomado de la web oficial del
INAMHI, http://www.serviciometeoro-
logico.gob.ec/cambio-climatico/ ).
Diferencia de medias entre las dos
muestras:
X: promedios de las radiaciones solares
en cada hora-día de la época lluviosa.
Y: promedios de las radiaciones solares
en cada hora-día de la época seca.
Figura 5: muestras de promedios de
radiación solar en cada hora-día en las
épocas lluviosa y seca.
Diseño de muestras
independientes
Método
Paramétrico
Método
Bootstrap
Muestras grandes
con suposiciones a,
b y c
Aplicable con estadísti-
co Z normal estándar
Aplicable sin
supuestos
Muestras pequeñas
con suposiciones a,
b, c, d y e
Aplicable con estadís-
tico t de la distribución
t-Student
Aplicable sin
supuestos
Muestras con falta
de normalidad
No aplicable Aplicable
ISSN 1390-5740 Número 17 Vol. 1 (2017)
ISSN 2477-9105

R
eferencias
73
Prueba de normalidad de las muestras:
El test de normalidad se realizó con
Shapiro-Wilk (4,5,7), aplicando a X se
obtiene un p-valor = 0.1376 que acepta la
normalidad con una confianza del 95%.
Mientras que este test aplicado a Y da un
p-valor = 0.034 rechaza la normalidad
con una confianza del 95 %.
En este caso no se puede aplicar el mé-
todo Paramétrico común, por tanto se
procede a aplicar el método Bootstrap
propuesto.
Prueba de hipótesis:
1. H
0
: μ
1
- μ
2
= 0 (hipótesis nula: dife-
rencia de medias igual a 0)
2. Nivel de significancia α = 0.05
3. El criterio de aceptar H
0
es cuando el
0 pertenece al intervalo de confianza
Bootstrap, caso contrario la hipóte-
sis nula es rechazada.
4. El intervalo de confianza Bootstrap
al 95 % se calculó siguiendo los pa-
sos del algoritmo del método Bootstrap propuesto
(con 1000 réplicas):
- 259.5 < μ
1
- μ
2
< 189.7 (9)
5. Decisión: En la ecuación 9 se observa que el intervalo
de confianza Bootstrap contiene el 0, por lo que H
0
no se rechaza, es decir que las medias de las variables
X e Y son significativamente iguales al 95 % de con-
fianza.
CONCLUSIONES
EL método Bootstrap propuesto es una nueva alternativa
científica para hipótesis concernientes a la diferencia de
medias en variables independientes.
La falta de condición de normalidad y de tamaños de las
muestras en el método Bootstrap propuesto, hace que este
sea muy flexible y ampliamente aplicable, a diferencia del
método Paramétrico.
AGRADECIMIENTOS
A los directivos de la Estación Meteorológica de la Fa-
cultad de Ciencias de la Escuela Superior Politécnica de
Chimborazo.
A la SENESCYT.
1. Davison AC, Hinkley DV. Bootstrap Methods and their Application. Cambridge University
Press; 1997.
2. Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other
measures of statistical accuracy. Statistical Science 1; 1986.
3. Johnson R. Probabilidad y estadística para ingenieros. Vol 1. 8a ed. México: Pearson educación;
2012.
4. Patrick, R. 1982. An extension of Shapiro and Wilk's W test for normality to large samples.
Applied Statistics, 31, 115–124.
5. Patrick, R. 1982. Algorithm AS 181: The W test for Normality. Applied Statistics, 31, 176–180.
6. Rizzo M.L. Statistical Computing with R. Chapman&Hall/CRC; 2008.
7. Thode H. Testing for Normality. Marcel Dekker, Inc; 2002.
8. Vélez R, García A. Principios de inferencia estadística. UNED. 1993.
9. Wasserman L. All of Statistics. A Concise Course in Statistical Inference. Springer; 2006.
Meneses, Zuñiga, Haro