
R
esumen
A
bstract
4
ISSN 2477-9105 Número 21 Vol. 1 (2019)
NORMALIDAD.
1
Pablo Flores Muñoz*,
2
Laura Muñoz Escobar,
1
Tania Sánchez Acalo
* p_flores@espoch.edu.ec
Most parametric tests are subject to normality. There are forty different tests to prove this
assumption. Preliminary researches to determine the best tests are based on the estimation of their
power using samples from known non-normal distributions but whose distance or contamination
from normality is unknown. In the present study, we selected seven better and more known tests.
Through a simulation process, we estimate the power of each one using samples from unknown
distributions but with a measurable distance from normality. It seems that Shapiro - Wilk test is the
best option, its power is very high, but only for large non-normal samples and strong distances. For
distributions with weak distances and small samples it seems that none of the traditional tests are
good. We discuss a possible poor approach to these tests and their impact on the results obtained.
Finally, the possibility of including a hypothesis test based on the equivalence approach is analyzed;
perhaps this option is better than the traditional tests introduced.
keywords: Normality test, Power, Fleishman Coefficients, Equivalence, Simulation.
La mayoría de pruebas de hipótesis paramétricas están sujetas al cumplimiento de normalidad.
Debido a la gran variedad de opciones para contrastar este supuesto, se considera como mejor
alternativa el test que presente una mayor potencia. Investigaciones preliminares estiman este valor
a partir de muestras provenientes de distribuciones no normales conocidas pero cuyo alejamiento
o contaminación respecto a la normalidad se desconoce. En el presente estudio seleccionamos
siete pruebas que además de ser las más comunes parecen ser las mejores. Mediante un proceso
de simulación, estimamos la potencia de cada una de ellas usando muestras provenientes de
distribuciones desconocidas, pero con un alejamiento medible de la normalidad. Parece ser que el
test de Shapiro – Wilk es la mejor opción, su potencia es muy elevada, pero solo para muestras no
normales grandes y alejamientos fuertes. Para distribuciones con alejamientos débiles y muestras
pequeñas parece ser que ninguna de las pruebas tradicionales en estudio es buena. Se discute un
posible mal planteamiento de estos test y su incidencia en los resultados obtenidos. Finalmente se
introduce la posibilidad de incluir pruebas basadas en el enfoque de equivalencia, las cuales quizás
podrían resultar mejores que las pruebas estudiadas.
Palabras claves: Pruebas de normalidad, Potencia, Coeficientes de Fleishman, Equivalencia, Simu-
lación.
Fecha de recepción: 27-12-2018 Fecha de aceptación: 25-01-2019
STUDY OF THE POWER OF TEST FOR NORMALITY USING UNKNOWN
DISTRIBUTIONS WITH DIFFERENT LEVELS OF NON NORMALITY.
ESTUDIO DE POTENCIA DE PRUEBAS DE NORMALIDAD USANDO
DISTRIBUCIONES DESCONOCIDAS CON DISTINTOS NIVELES DE NO
1
Escuela Superior Politécnica de Chimborazo, Facultad de Ciencias, Grupo de Investigación
en Ciencia de Datos, Riobamba, Ecuador
2
Universidad Nacional de Chimborazo, Facultad de Ciencias de la Educación, Humanas y
Tecnologías, Riobamba, Ecuador

5
I. INTRODUCCIÓN
La mayoría de técnicas utilizadas para
realizar inferencia estadística (prue-
bas de hipótesis, análisis de regresión,
modelos de pronósticos, etc.) se basan
en modelos paramétricos, los cuales a
su vez están sujetos principalmente al
cumplimiento del supuesto de norma-
lidad. En la literatura estadística, varias
pruebas de hipótesis se han propuesto
con la nalidad de probar si un grupo
de datos provienen o no de esta distri-
bución teórica, de hecho, los trabajos de
revisión reportan aproximadamente 40
test diferentes desarrollados con este n
(1,2,3).
Ante esta diversa gama de opciones,
suponemos que la interrogante más
frecuente con la que se encuentra un
investigador que usa instrumentos es-
tadísticos paramétricos tiene que ver
con cuál es la mejor alternativa para
probar el supuesto de normalidad en
sus datos. En este sentido, múltiples
investigaciones se han desarrollado
con el fin de establecer un criterio de
comparación que permita determinar
objetivamente cuál opción es la más
adecuada (4,5,6,7).
El criterio de comparación que usan
estas investigaciones se basa en estimar
mediante un proceso de simulación la
potencia que tienen las distintas prue-
bas con el fin de recomendar aquellas
cuya potencia resulte ser la más alta,
es decir aquella prueba que maximice
la probabilidad de rechazar la hipóte-
sis nula de existencia de normalidad
cuando realmente esta es falsa. Para
asegurar esta condición de no norma-
lidad, los trabajos mencionados usan
muestras provenientes de distribucio-
nes conocidas (gamma, exponencial, t
– Student, uniforme, etc.)
En (6), se estimó la potencia de 33
pruebas de normalidad para distintos
tamaños muestrales (n=25,50,100) y niveles de signi-
ficancia (α=0.05,0.10), además con el fin de asegurar la
condición de no normalidad en las muestras generadas
utilizó distintas distribuciones no normales simétricas
(Beta, Cauchy, Laplace, Logística, t – Student), asimé-
tricas (chi - cuadrado, Gamma, Gumbelt, Log - Nor-
mal, Weibull) y normales modificadas (normal trun-
cada, normal contaminada, normal mezclada y normal
con atípicos).
La potencia estimada en todos estos casos no se alte-
ra significativamente cuando el nivel de significancia
es diferente y no se pudo definir alguna prueba en es-
pecífico como más potente, puesto que existen varias
opciones diferentes que dependen de la naturaleza de
la no normalidad. Otro estudio más detallado que el
anterior, el cual usa las mismas distribuciones teóri-
cas para simular muestras no normales, determinó que
para muestras simétricas, Shapiro – Wilk junto con
Jarque – Bera son los test más potentes, mientras que
paras muestras asimétricas Shapiro – Wilk y Anderson
– Darling parecen ser la mejor opción (7). En tra inves-
tigación, usando tamaños muestrales (n=20,30,40,50),
se determinó que si se generan muestras a parir de una
Distribución Beta, el test más potente es Anderson –
Darling, si las muestras son generadas por una Gamma
o por una Log – normal, el test más potente es Jarque
– Bera (5).
Todos estos estudios, tienen en común que para estimar
la potencia generan muestras de distribuciones de pro-
babilidad que, aunque es verdad que no son normales,
muchas de ellas tienden a serlo de manera asintótica, lo
cual creemos puede estar afectando de alguna manera
los resultados encontrados. Además, pensamos que en
un análisis real no necesariamente los datos disponibles
deben ajustarse a alguna distribución no normal cono-
cida como las presentadas en estudios previos, sino que
en algunos casos (o quizás en la mayoría) tendrán una
distribución totalmente desconocida. Aunque la gene-
ración de muestras desconocidas, a nuestro parecer es
tan importante como aquellas que provienen de distri-
buciones conocidas, estas no se han presentado en nin-
guna de las investigaciones antes mencionadas. Es así
que proponemos el siguiente estudio, donde mediante
un proceso de simulación estocástica estimamos la po-
tencia de siete pruebas de normalidad, usando el siste-
ma de Fleishman (8) para la creación de muestras de
distribución desconocida (pero que se sabe se encuen-
tran en datos reales) con distintos niveles de alejamiento
o contaminación de la normal.
Flores, Muñoz, Sánchez

6
ISSN 2477-9105 Número 21 Vol. 1 (2019)
Con
ba
Xx
i
n
i
ni
i
=−
=
−−
()
∑
1
1
y
amVmVm
i
=
()
′′
−−
−
11
12
/
. Donde,
Xx
ni
i
−−
()
−
1
son las diferencias suce-
sivas que se obtiene al restar el primer
valor al último valor, el segundo al ante-
penúltimo y así sucesivamente.
a
i
, son
los coeficientes tabulados en la tabla de
Shapiro,
mm m
n
=…
()
1
,,
son los valores
medios del estadístico ordenado, de va-
riables aleatorias independientes e idén-
ticamente distribuidas, muestreadas de
distribuciones normales.
V
es la matriz
de covarianzas de ese estadístico de or-
den.
Se rechazará
H
0
�
si
WW
n
≤
∝,
, donde
W
n∝,
son los puntos críticos tabulados
en (12).
Test de Anderson – Darling (13)
Sea
XX X
n12
,,...,
una muestra aleatoria
de tamaño mayor que 5, el estadístico de
prueba para este test viene dado por:
A
iZZ
n
n
i
n
ini
2
1
1
21
=−
−
()
()
+
()
()
−
=
+−
∑
ln ln
Donde
Z
i
es el cuantil de una distribu-
ción de probabilidad acumulada de una
distribución normal estándar. De acuer-
do al nivel de significancia y tamaño de
muestra, rechazamos la hipótesis de
normalidad cuando
A
2
es mayor que
A
c,
α
2
,donde
A
c,
α
2
son los puntos críticos
tabulados en (14).
Test de Jarque – Bera (15)
Sea
XX X
n12
,,...,
una muestra aleato-
ria, el estadístico de prueba para este test
viene dado por:
JB
n
S
k
=+
−
()
2
2
6
3
24
II. MATERIALES Y MÉTODOS
REVISIÓN DE PRUEBAS DE NORMALIDAD
Tomando en cuenta los resultados de investigaciones
previas y considerando los test de normalidad más co-
munes en la mayoría de libros y software estadístico, pro-
ponemos el estudio de potencia de las siguientes pruebas
para contrastar las hipótesis:
H
0
:
Los datos provienen de una distribución normal
H
1
:
Los datos no provienen de una distribución normal
Prueba de Kolmogorov – Smirnov (9; 10)
Sea
XX X
n12
() ()
()
…,,,
una muestra ordenada aleatoria,
con función de distribución acumulada
Fx
i
()
()
, con
1
≤
()
≤
in
, y sea
Z
i
la distribución de probabilidad
acumulada de una distribución normal estándar. El
estadístico de prueba para este test viene dado por:
DD
D=
()
+−
max,
Donde,
DF
xZ
i
i
+
()
=
()
−
{}
max
y
DZFx
i
i
−
()
=−
()
{}
ma
x'
. Se rechaza
H
0
. cuando
Dd≥
siendo
d
los puntos críticos que se encuentran
en la tabla
tabulada (9).
Test de Lilliefors (11)
Esta prueba es una modificación de Kolmogorov-Smir-
nov. Se sabe de antemano que KS es apropiada cuando
se conoce los parámetros de la distribución hipotética
(normal), sin embargo a veces o casi siempre es difícil
conocer estos valores. En este sentido, el test Lilliefors usa
las estimaciones de μ y σ en función de los datos de la
muestra. El estadístico y los valores críticos siguen siendo
los mismos que KS.
Test de Shapiro – Wilk (12).
Sea
XX X
n12
,,...,
una muestra aleatoria, el estadístico de
prueba para este test viene dado por:
W
b
xx
i
n
i
=
−
()
=
∑
2
1
2

7
OBTENCIÓN DE MUESTRAS PROVENIENTES DE
DISTRIBUCIONES DESCONOCIDAS.
Allen Fleishman, en el año 1978, desarrolló un método
mediante el cual se pueden generar muestras aleatorias
no normales cuya distribución se desconoce (8). Partien-
do de una normal estándar
Z
(
ZN
~,
µσ
==
()
01
), el
autor demostró que una transformación lineal de esta va-
riable, de la forma
YabZ cZ dZ=+ ++
23
, sigue una dis-
tribución totalmente desconocida de parámetros
µσγγ
==
()
01
12
,,,
, donde
γ
1
y
γ
2
representan respecti-
vamente los coeficientes poblacionales de simetría y cur-
tosis, los cuales a su vez definen los grados de separación
o contaminación de la normal.
En una posterior investigación (18), donde se recopiló
693 variables con distribución desconocida, provenien-
tes de bases de datos reales (de las cuales 193 correspon-
dieron a poblaciones diferentes), se estimó los coeficien-
tes γ
1
de simetría y γ
2
de curtosis basados en el tercer y
cuarto momento no central respectivamente. Los resul-
tados mostraron un rango de valores para γ
1
compren-
dido entre -2.49 y 2.33, mientras que para γ
2
los valores
encontrados fluctuaban en un intervalo de -1.92 a 7.41.
Establecer puntos de corte para valores combinados de
estos coeficientes permitió determinar diferentes niveles
de alejamiento o contaminación de la normalidad.
Con la ayuda de funciones existentes en el software esta-
dístico R (19), en el presente estudio utilizamos la trans-
formación de Fleishman para generar muestras prove-
nientes de distribuciones desconocidas. Los valores para
los coeficientes (a,b,c,d) son determinados de acuerdo
a los valores γ
1
y γ
2
propuestos a partir de las investi-
gaciones desarrolladas en (18,20). Estos coeficientes se
obtuvieron con la función “fleishman.coef” del paquete
“BinNonNor” (21). Los valores de simetría, curtosis y
coeficientes de Fleishman calculados con sus respectivos
niveles de alejamiento de la normalidad, se muestran en
la Tabla 1.
Nivel de
Contami-
nación
Simetría Curtosis
Coecientes de
Fleishman
Leve
0.25 0.7
(-0.037, 0.933,
0.037, 0.021)
Moderada
0.7 1
(-0.119, 0.956,
0.119, 0.0098)
Donde,
S
representa el coeficiente de
asimetría y
�k
el coeficiente de curtosis.
La hipótesis nula de normalidad se re-
chaza cuando
JB JB
c
>
,
α
, donde
JB
c,
α
es el valor crítico de una distribución chi
– cuadrado, que deja a la derecha un
área de α con 2 grados de libertad.
Test de Bondad de Ajuste
χ
2
(16)
Sea
XX X
n12
,,...,
una muestra aleatoria
de tamaño mayor que 5, el estadístico de
prueba para este test viene dado por:
χ
2
1
2
=
−
()
=
∑
i
k
ii
i
OE
E
Donde,
k
es el número de clases exis-
tentes,
O
i
son las frecuencias observa-
das en cada clase y
E
i
son las frecuen-
cias esperadas. La hipótesis nula de
normalidad se rechaza cuando
χχ
22
>
a
,
donde
χ
a
2
es el valor crítico de una dis-
tribución chi cuadrado con
k −1
grados
de libertad que deja a la derecha un área
de α.
Test de Cramer – Von Mises (17).
Sea
XX X
n12
,,...,
una muestra aleatoria
de tamaño mayor que 5, el estadístico de
prueba para este test viene dado por:
W
n
p
i
n
i
n
i
=+ −
−
=
∑
1
12
21
2
1
2
Donde
p
xx
s
i
i
=
−
φ
, siendo
φ
la fun-
ción de distribución acumulada de una
distribución normal estándar y además
x �
y
s�
representan respectivamente la
media y desviación estándar muestral.
Los valores críticos son calculados a par-
tir del estadístico modificado
ZW
n
=+
1
05.
, de acuerdo a la Tabla
4.9 presentada en (2).
Flores, Muñoz, Sánchez
8
ISSN 2477-9105 Número 21 Vol. 1 (2019)
Alta
1.3 2
(-0.249, 0.984,
0.249, -0.016)
Severa
2 6
(-0.314, 0.826,
0.314, 0.023)
Tabla 1. Simetría, Curtosis y coecientes de Fleishman usados para
generar muestras no normales.
MÉTODO DE ESTIMACIÓN DE LA POTENCIA.
La potencia fue estimada a partir de una función pro-
pia de R, la cual implementa un algoritmo de simu-
lación de montecarlo para dicho fin. El algoritmo
consiste en crear muestras no normales de tamaño
n=5,10,15,20,30,50,100, a partir de la transformación
de Fleishman (usando los coeficientes dados en la Ta-
bla 1.), luego las siete técnicas descritas en la Sección II
para probar la hipótesis de normalidad son aplicadas
sobre estas muestras, finalmente nos interesará guardar
en un vector, un valor lógico que indique “TRUE” si la
hipótesis se rechaza o “FALSE” en caso contrario. Este
proceso se repite m=100000 veces y la potencia queda
estimada como la proporción de rechazos de la hipótesis
nula. Dado que en investigaciones previas se comprobó
que los resultados de la potencia son independientes del
nivel de significancia, el valor α usado en cada una de las
pruebas fue de 0.05.
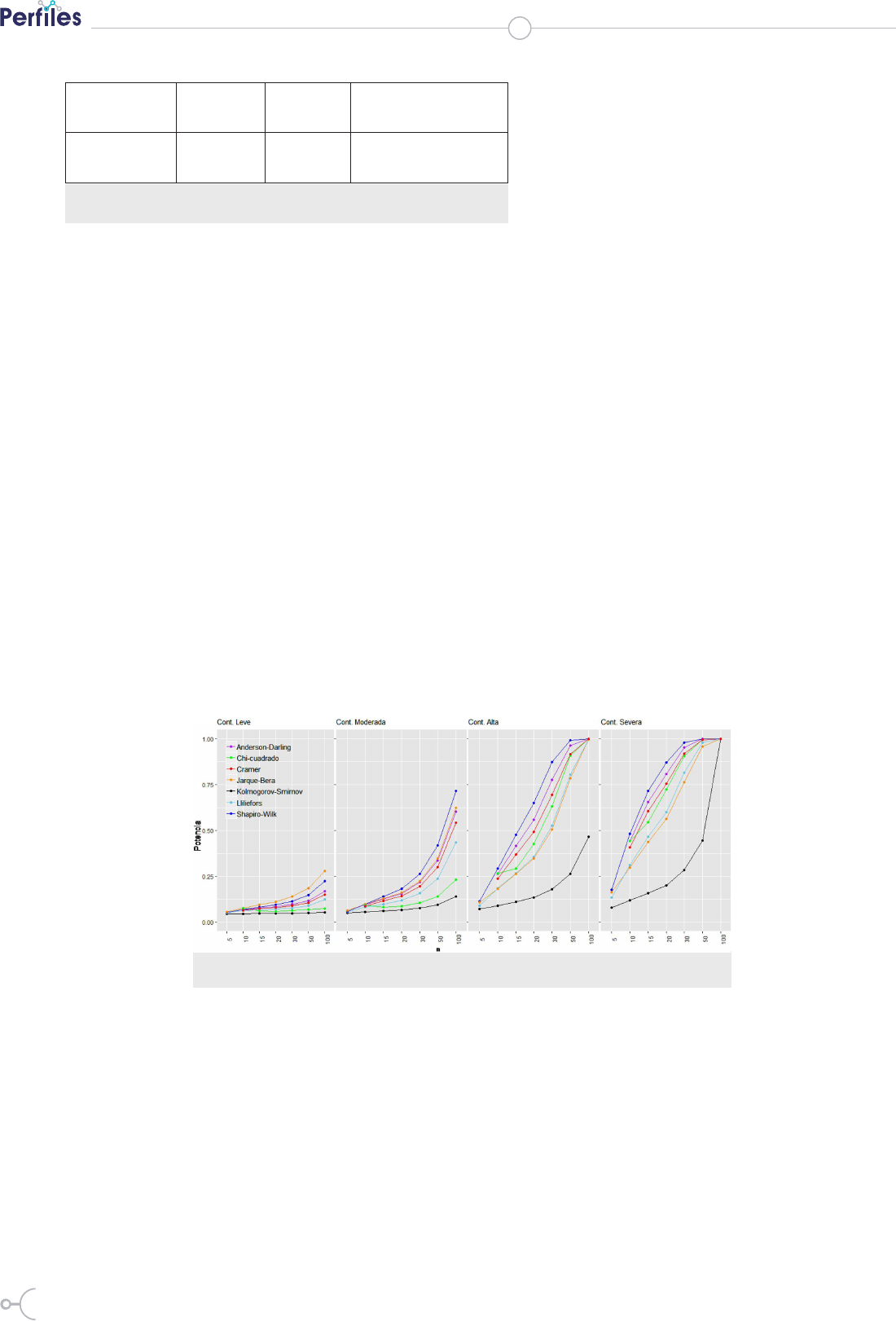
III. RESULTADOS
La Figura 1, resume la potencia deter-
minada para cada una de las pruebas de
normalidad para diferentes alejamien-
tos de la distribución y distinto tamaño
muestral.
De manera general, en todos los esce-
narios analizados se puede observar un
comportamiento casi invariante de las
potencias calculadas. Esta potencia se
incrementa conforme aumenta el grado
de alejamiento de la normal y el tama-
ño muestral crece, de este modo, por
ejemplo para una contaminación leve y
un tamaño muestral de 5, la potencia de
todas las siete pruebas es demasiado baja
(tiende al nivel de significancia 0.05),
mientras que en el otro extremo, es decir
cuando existe una contaminación severa
y el tamaño muestral es 100, la potencia
de todas las pruebas tiende a 1 (nivel de
potencia más grande que puede alcanzar
una prueba).
De manera específica, cuando la contaminación es leve,
se puede observar que no muy distante de la Prueba de
Shapiro – Wilk, el test de Jarque – Bera parece tener la
potencia más alta independientemente del tamaño mues-
tral usado, sin embargo, esta potencia decrece conforme
el nivel de contaminación aumenta y a partir de un ale-
jamiento moderado, la prueba de Shapiro Wilk parece
ser la más potente de todas, por lo se recomienda su uso.
Contrario a esto, independientemente del alejamiento y
el tamaño muestral, la prueba de Kolmogorov – Smirnov
Figura 1. Potencia para diferentes niveles de contaminación, distintos tamaños
muestrales y α=0.05
resulta ser siempre la peor y se desacon-
seja su uso. Los demás test analizados
(Anderson D, Chi – cuadrado, Cramer y
LLilefors), siempre se encuentran entre
los dos test más y menos potentes des-
critos.
IV. DISCUSIÓN
Los resultados obtenidos muestran evi-

9
do al enunciado de Box, tendría más sentido que en lugar
de probar normalidad perfecta, se contraste una hipóte-
sis que pruebe la existencia de una normalidad aproxi-
mada, es decir una normalidad que acepte desviaciones
tan pequeñas que se puedan considerar despreciables o
irrelevantes. Aunque es nuevo y no tan común, este en-
foque para contrastar hipótesis, distinto al enfoque tradi-
cional, estudiado en la mayoría de la literatura estadísti-
ca existe y se denomina “pruebas de equivalencia” (23).
Entendemos por equivalencia a una forma dilatada de
una relación de identidad, la cual se induce al añadir en
la hipótesis tradicional una zona de irrelevancia alrede-
dor del correspondiente punto en el espacio paramétrico
que denota perfecta normalidad, este enfoque conduce a
diseñar un estudio que pretende demostrar ausencia de
una diferencia relevante entre los efectos de dos distri-
buciones comparadas (una de ellas podría ser la normal),
es decir equivalencia. En este sentido, resulta interesante
la realización de investigaciones futuras sobre estimación
de la potencia pero incorporando el criterio de equiva-
lencia, de hecho existen ciertos estudios donde ya se de-
muestra la superioridad de este enfoque sobre el tradi-
cional (24). Podría ser, que este criterio de equivalencia
sea más potente, pero eso no lo sabremos hasta que se
realicen las mediciones respectivas.
V. CONCLUSIONES
A diferencia de otras investigaciones, donde para asegu-
rar la no existencia de normalidad teórica, se usa distri-
buciones no normales conocidas, en el presente trabajo
se usó el sistema de Fleishman, el cual nos permitió crear
muestras no normales con un grado medible del aleja-
miento o contaminación. Este nuevo aporte para estudiar
la potencia de las pruebas de normalidad, permitió tener
la seguridad de que las muestras provienen de una dis-
tribución desconocida, independientemente del tamaño
muestral, lo cual podría inuir en una normalidad asin-
tótica. Además, de esta forma se pudo obtener grados de
contaminación a partir de los cuales se presenta una po-
tencia relativamente alta, lo cual permitió detectar grados
de alejamientos que se pueden considerar irrelevantes.
Luego de comparar la potencia de siete pruebas de hipó-
tesis para contrastar normalidad, hallamos que Shapiro
– Wilk es el test más potente. Por tanto, esta prueba maxi-
miza la probabilidad de cometer un acierto en el sentido
de rechazar la hipótesis de normalidad perfecta dado que
teóricamente esta es falsa. Sin embargo, la potencia de
esta prueba es óptima siempre y cuando el tamaño mues-
tral sea mayor que 30 (n≥30) y para contaminaciones de
Flores, Muñoz, Sánchez
dencia a favor del uso del test de Shapi-
ro Wilk, el cual parece tener una mayor
potencia respecto a los otros test anali-
zados. Sin embargo, es muy importante
hacer notar que, aunque este test es re-
lativamente alto en todos los tamaños
muestrales, en realidad en el intervalo
[0, 1] donde toma valores, nunca supera
un valor que podría ser aceptable (míni-
mo de 0.8) para muestras pequeñas. A
partir de una contaminación alta, solo
se observa una potencia elevada para el
tamaño muestral n≥30. Esto parece ser
razonable y coherente ya que solo esta-
mos confirmando algo que en estadísti-
ca suele ser muy común “todas las co-
sas mejoran cuando aumenta el tamaño
muestral”.
Llama la atención, lo poco (o casi nada)
potentes que resultan ser todas las prue-
bas analizadas cuando existe una con-
taminación leve o moderada, en este
sentido podemos concluir que los test
de normalidad solo pueden ser buenos
cuando el alejamiento de la distribu-
ción teórica es fuerte, mientras que, para
muestras con alejamientos débiles, estas
pruebas tradicionales están lejos de ser
efectivas. A nuestro criterio, lo que po-
dría estar ocurriendo es que las muestras
generadas con alejamiento leve y mode-
rado, presentan un grado de contami-
nación tan pequeño que podría consi-
derarse despreciable o irrelevante como
para ser consideradas no normales.
Si analizamos un poco más a fondo, la
hipótesis nula de los test en estudio su-
giere que los datos siguen una normali-
dad perfecta, al respecto George Box en
1979 dijo “En la vida real no existe una
distribución perfectamente normal, sin
embargo, con modelos que se sabe que
son falsos, a menudo se puede derivar
resultados que coinciden, con una apro-
ximación útil a los que se encuentran en
el mundo real” (22). Entonces, según
este enunciado, no tiene sentido realizar
test de hipótesis que prueben una per-
fecta normalidad (ya sabemos que esto
no existe). A nuestro criterio y de acuer-

10
ISSN 2477-9105 Número 21 Vol. 1 (2019)
1. Recent and classical tests for normality-a comparative study. Baringhau, L, Danschke, R y Henze,
N. 1, 1989, Communications in Statistics-Simulation and Computation, Vol. 18.
2. D’Agostino, Ralph y Stephens, Michael. Goodness-of-t techniques (Statistics, a series of text-
books and monographs. New York : Marcel Deker, 1986.
3. Tests of unvariate and multivariate normality. Mardia, Kanti. 1980, Handbook of statistics, Vol.
1.
4. Simulation based nite sample normality test in linear regressions. Dufour, Jean-Marie, y otros.
1998, Econometrics Journal, Vol. 1.
5. A comparison of various tests of normality. Yazici, Berna y Yolacan, Senay. 2, 2007, Journal of
Statistical and Simulation, Vol. 77.
6. An empirical power comparison of univariate goodness of t test for normality. Romao, Xavier,
Delgado, Raimundo y Costa, Aníbal. 5, May de 2010, Journal of Statistical Computation and Si-
mulation, Vol. 80.
7. Comparisons of various types of normality tests. Yap, B y Sim, C. 12, December de 2011, Journal
of Statistical Computation and Simulation, Vol. 81.
8. A method for simulating non-normal distributions. Fleishman, Allen. 4, 1978, Psycometrika,
Vol. 43.
9. Sulla determinazione empirica di una lgge di distribuzione. Kolmogorov, Andrey. 1933, Inst. Ital.
Attuari, Giorn., Vol. 4.
10. Table for estimating the goodness of t of empirical distributions. Smirnov, Nickolay. 2, 1948,
e annals of mathematical statistics, Vol. 19.
11. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Lilliefors,
Hubert. 318, 1967, Journal of the American statistical Association, Vol. 62.
12. An analysis of variance test for normality. Shapiro, SS y Wilk, MB. 3, 1965, Biometrika, Vol. 52.
13. Asymptotic theory of certain" goodness of t" criteria based on stochastic processes. Anderson,
eodore y Darling, Donald. 1952, e annals of mathematical statistics}, Vol. 23.
14. EDF statistics for goodness of t and some comparisons. Stephens, Michael. 347, 1974, Journal
of the American statistical Association, Vol. 69.
15. Ecient tests for normality, homoscedasticity and serial independence of regression residuals.
Jarque, Carlos y Bera, Anil. 3, 1980, Economics Letters, Vol. 6.
16. Greenwood, Priscilla y Nikulin, Michael. A guide to chi-squared testing. 280. s.l. : John Wiley
& Sons, 1996.
17. On the composition of elementary errors: First paper: Mathematical deductions. Cramér, Ha-
rald. 1928, Scandinavian Actuarial Journal, Vol. 1.
18. Skewness and kurtosis in real data samples. Blanca, María, y otros. 2013, Methodology.
19. R: A Language and Enviroment for Statistical Computing. Team, R Core. 2018, R Foundation
For Statistical Computing. https://www.R-project.org.
R
eferencias
normalidad alta y severa.
Para contaminaciones leves y moderadas, a pesar que la
potencia del test de Shapiro – Wilk es la más alta, no se
puede considerar que es óptima, puesto que en ningún
caso supera al menos un valor razonable de 0.80. Parece
ser que estas dos contaminaciones de la normalidad, son
alejamientos que podrían considerarse
tan irrelevantes que se podrían despre-
ciar.
Un planteamiento hipotético de norma-
lidad irrelevante en lugar de normalidad
perfecta podría ser una mejor alternati-
va.

11
20. Comparison of the procedures of Fleishman and Ramberg et al. for generating non-normal data
in simulation studies. Bendayan, Rebecca, y otros. 1, 2014, Annals of Psychology, Vol. 30.
21. BinNonNor: Data Generation with Binary and Continuous Non-Normal Components. Inan,
Gul y Demirtas, Hakan. 2018, R package version 1.4.
22. Robustness in the strategy of scientic model building. Box, George. 1979, Army res o Work
Robustness, Vol. 1.
23. Wellek, Sthepan. Testing St atistical Hypothesis of equivalence and non Inferiority. 2010.
24. Heteroscedasticity Irrelevance when Testing Means Dierence. Flores, Pablo y Ocaña, Jordi. 1,
June de 2018, SORT, Vol. 42.
25. EDF statistics for goodness of t and some comparisons. Stephens, Michael. 1974, Journal of the
American statistical Association, págs. 730--737.
Flores, Muñoz, Sánchez