
87
UNA TÉCNICA DE AGRUPACIÓN ROBUSTA PARA UN ENFOQUE BIG
DATA: CLARABD PARA TIPOS DE DATOS MIXTOS
1,2,3
Víctor Morales-Oñate,
4
Bolívar Morales-Oñate
1
Instituto de Estadística, Universidad de Valparaíso, Valparaíso, Chile
2
Departamento de Desarrollo, Ambiente y Territorio, Facultad Latinoamericana de Ciencias So-
ciales, Quito, Ecuador
3
Analítica de Datos, IDCE Consulting, Quito, Ecuador
4
Facultad de Ciencias, Escuela Superior Politécnica de Chimborazo, Riobamba - Ecuador.
*bolivar.morales@espoch.edu.ec
A
bstract
When a researcher does not have an a priori knowledge of the configuration of groups in a given
data set, the need to perform a classification known as unsupervised classification emerges. In
addition, the data set can be mixed (qualitative and/or quantitative data) or presented in large
volumes. The kmeans algorithm, for example, does not allow the comparison of mixed data and
is limited to a maximum of 65536 objects in the R software. K-medoids, on the other hand, allows
the comparison of mixed data but also has the same limitation of objects that k-means does. The
traditional CLARA algorithm can easily exceed this volume limitation, but it does not allow the
comparison of mixed data. In this context, this work is an extension of the CLARA algorithm for
mixed data, the CLARABD algorithm. Gower distance is central in CLARABD to make this ex-
tension, because it allows the comparison of mixed data and it is also possible to process a data set
with more than 65536 observations. To show the benefits of the proposed algorithm, a simulation
process has been carried out as well as an application to real data, obtaining consistent results in
each case.
Palabras clave: Classification, CLARA, K medoids, mixed data types, R software.
A robust clustering technique for a Big Data approach: CLARABD for Mixed data types
Cuando el investigador no cuenta con un conocimiento apriori de la conformación de grupos en un
conjunto de datos dado, emerge la necesidad de realizar una clasificación conocida como clasificación
no supervisada. Además, el conjunto de datos puede ser mixto (datos cualitativos y/o cuan- titativos)
o presentarse en grandes volúmenes. El algoritmo k-medias, por ejemplo, no permite la comparación
de datos mixtos y está limitado a un máximo de 65536 objetos en el software R. K-medoides, por su
parte, permite la comparación de datos mixtos pero también tiene la misma limitación de objetos que
k-medias. El algoritmo CLARA tradicional puede exceder fácilmente este limitante de volúmenes,
pero no permite la comparación de datos mixtos. En este contexto, este trabajo es una extensión del
algoritmo CLARA para datos mixtos, el algoritmo CLARABD. La distancia de Gower es central en
CLARABD para realizar esta extensión, debido a que permite la comparación de datos mixtos y también
es posible procesar un conjunto de datos con mas de 65536 observaciones. Para mostrar las bondades
del algoritmo propuesto, se ha realizado un proceso de simulación así como una aplicación a datos reales
obteniendo resultados consistentes en cada caso.
Palabras clave: Clasificacion, CLARA, K-medoides, datos mixtos, R software.
R
esumen
Fecha de recepción: 11-01-2019 Fecha de aceptación: 11-06-2019
V. Morales, B.Morales

88
ISSN 2477-9105 Número 22 Vol. 2 (2019)
I. INTRODUCCION
La búsqueda de grupos en un conjunto de datos no es una
tarea nueva. Uno de los libros seminales a este respecto
fue publicado por primera vez en 1990, Finding groups
in data: An introduction to cluster analysis [1]. Lo que en
ese entonces se conoce en inglés como cluster analysis se
traduce al español como análisis de conglomerados. Co-
múnmente se podía encontrar estos métodos en trabajos
relacionados a estadística multivariante [2]. Hoy, con el
surgimiento de la ciencia de datos y del big data [3], el
análisis de conglomerados se conoce como clasicación
no supervisada o aprendizaje no supervisado, llevando este
nombre debido a que el investigador no conoce apriori,
la clase o grupo al que pertenecen las observaciones del
conjunto de datos que analiza.
La investigación teórica y aplicada que usa algoritmos de
clasicación no supervisada sigue vibrante. Por ejemplo,
existen trabajos en diferentes áreas como clasicación de
imágenes [4], analítica de deportes [5], análisis de lengua-
je [6] y ciencias sociales [7] en esta línea de investigación.
Cada uno usa diferentes métodos con un mismo propó-
sito: encontrar grupos en los datos analizados. Dos de los
algoritmos clásicos con los que se ha abordado este pro-
blema son k-medias y k-medoides. Ambos tienen como
entrada el conjunto de datos y el número de conglome-
rados, como salida una partición del conjunto. K-medias
permite usar únicamente variables cuantitativas y kme-
doides permite usar variables cuantitativas y cualitativas.
Una extensión de este ´ultimo es el algoritmo CLARA [1].
CLARA es conocida por ser una alternativa robusta para
clasicación no supervisada para conjuntos de datos
grandes. Por un lado, se considera robusta por usar el al-
goritmo k-medoides para obtener los representantes de
los grupos. Por otro lado, un conjunto de datos es consi-
derado grande en función de la complejidad computacio-
nal así como del poder de cómputo. Por ejemplo, en 1990
se entendía como un conjunto de datos grande cuando se
tenía más de 100 observaciones [1].
Hoy se considera grande un problema con varios miles de
observaciones. En particular, el soware R permite hasta
65536 observaciones cuando usa el algoritmo k-medoides
tradicional; más allá de ese umbral el problema debe ser
abordado con el algoritmo CLARA [8]. En el contexto Big
Data, CLARA es un algoritmo que encaja adecuadamen-
te. Es capaz de procesar conjuntos de datos de millones de
observaciones en pocos segundos [9]. Sin embargo, una
limitante es la métrica utilizada para el
cálculo de las disimilaridades (diferencia
o distancia). Actualmente las opciones
son la distancia euclideana y la de man-
hattan. Esto limita el uso de este potente
algoritmo para la clasicación de datos
mixtos, esto es, datos de tipo nominal,
ordinal y binario (a) simétricos.
El algoritmo CLARA realiza múltiples
muestras del conjunto de datos original,
aplica k-medoides a cada muestra, en-
cuentra los medoides y luego devuelve
su mejor agrupamiento como salida.
Este trabajo presenta el algoritmo CLA-
RABD que extiende al algoritmo tradi-
cional posibilitando la clasicación de
observaciones con tipos de datos mixtos
y ha sido implementado en el lenguaje
R [10]. Especícamente, esta propuesta
se diferencia del algoritmo CLARA tra-
dicional en que la entrada para el cálculo
de los medoides de cada muestra puede
realizarse mediante una matriz de dis-
tancias o disimilaridad con las métricas
euclídea, manhattan y gower. Siendo
esta última la métrica de disimilaridad la
que permite clasicar observaciones de
tipo mixto.
Marco Teórico
Es común encontrar deniciones de
clustering en la literatura de análisis
multivariante, machine learning y reco-
nocimiento de patrones. Se cita a conti-
nuación tres deniciones:
• Todo se relaciona con la agrupación o
segmentación de una colección de obje-
tos en subconjuntos o clúster, de modo
que aquellos dentro de cada clúster están
más estrechamente relacionados entre
sí que los objetos asignados a diferentes
clúster. [11]
• El clustering se reere a un conjunto
muy amplio de técnicas para encontrar
subgrupos, o clústeres, en un conjun-
to de datos. Cuando se agrupan las ob-

89
servaciones de un conjunto de datos, se
busca dividirlas en grupos distintos para
que las observaciones dentro de cada
grupo sean bastante similares entre sí,
mientras que las observaciones en di-
ferentes grupos son bastante diferentes
entre sí. [12]
• El análisis cluster, que es el ejemplo
más conocido de aprendizaje no super-
visado, es una herramienta muy popu-
lar para analizar datos multivariados no
estructurados. Dentro de la comunidad
de minería de datos, el análisis de clúster
también se conoce como segmentación
de datos, y dentro de la comunidad de
aprendizaje automático también se co-
noce como descubrimiento de clases.
La metodología consiste en varios al-
goritmos, cada uno de los cuales busca
organizar un conjunto de datos deter-
minado en subgrupos homogéneos, o
clúster. [13]
Sin embargo, es menos común encontrar
un marco unicador para el problema de
clasicación. En este sentido, [14] pre-
senta un marco que permite esta cone-
xión. Su propuesta se denomina Modelo
Estructural de Cubrimientos (MEC) y
ha motivado trabajos posteriores como
[15] y [16]. A continuación se revisa bre-
vemente los ítems más relevantes de su
teoría.
Denicion 1 (Estructura-Cubrimiento).
Una estructura-cubrimiento es una tu-
pla con los siguientes elementos: (Ω, ℜ,
δ, Q, π, f), donde
• Ω es un conjunto no vacío de objetos
Ω = {o
1
, o
2
, . . . , o
n
}.
• ℜ es un conjunto ℜ = {x
1
, x
2
,. . ., x
r
}
de variables llamadas Rasgos descripti-
vos, en función de los cuales se pueden
describir los objetos en Ω. Cada rasgo
descriptivo xi tiene un Dominio de de-
nición M
i
. Cada rasgo x
i
tiene un do-
minio D
i
.
• δ es una relación funcional δ : Ω →
(D
1
× D
2
× . . . × D
r
) llamada Relación de
Descripción que a cada objeto le asigna una descripción
en términos de los rasgos en ℜ.
• Q Es un conjunto Q = {C
1
, C
2
,. . ., C
k
}, de etiquetas co-
rrespondientes a conjuntos llamados Clases o Categorías,
en los cuales se agrupan los elementos de Ω.
• π es una relación funcional π : (Ω × Q) → [0, 1] lla-
mada Relacion de Pertenencia o Función de Pertenencia
que a cada pareja, (objeto, clase), le asocia un grado de
pertenencia.
• f es una relación funcional llamada Función de Analo-
gía entre Patrones. Es una función de comparación entre
patrones que puede ser de semejanza o diferencia.
La estructura-cubrimiento permite formalizar los dife-
rentes problemas de clasicación que el investigador pue-
de enfrentar. En cada tipo de problema se recibe como
datos iniciales algunos elementos de una estructura-cu-
brimiento, y se requiere encontrar los elementos faltan-
tes. Si el problema es supervisado, se conoce la familia de
clases y algunos elementos de pertenencia. Esto es, se
tiene Ω, ℜ, δ, Q, π (π se conoce parcialmente), pero no
se dispone de π ni f. Si, por el contrario, el problema es
no-supervisado, entonces, no se conoce más que los ob-
jetos y sus descripciones. Es decir, se tiene Ω, ℜ, δ, pero
no Q, π ni f.
El único elemento que está siempre ausente en todo pro-
blema de clasicación y que se convierte en el objetivo del
método, es determinar es la función de comparación en-
tre patrones. La selección de la función de comparación
es la decisión más importante en el proceso de solución
de un problema. En esa selección inuyen la experiencia
del modelador y las recomendaciones del experto.
Es adecuado mencionar también algunos tipos de cubri-
miento:
• Disjunto: Todas las clases son disjuntas.
• Solapado: Algunas clases se intersectan.
• Total: Todos los objetos pertenecen a a alguna clase.
• Parcial: No todos los objetos pertenecen a alguna clase.
Note que la función de comparación (semejanza o di-
ferencia) puede considerarse como la piedra angular del
MEC. En este sentido, existen diferentes formas de com-
parar objetos (también llamados patrones).
Denición 2 (Función de Comparación). Sean A y B dos
objetos en el espacio E,
A = (a
1
, a
2
,. . ., a
r
)
V. Morales, B.Morales

90
ISSN 2477-9105 Número 22 Vol. 2 (2019)
B = (b
1
, b
2
,. . ., b
r
)
entonces f(A, B) es una función de comparación de ob-
jetos tal que,
f : E × E → Γ.
Donde Γ es un conjunto totalmente ordenado
A partir de la denición 2, se derivan dos tipos de fun-
ciones de comparación: de semejanza y diferencia. Una
función de semejanza, donde el conjunto de salida es [0,
1], mide el grado de acuerdo, coincidencia o relación,
entre dos objetos, a partir del valor de cada uno de sus
atributos. Una función de diferencia, donde el conjunto
de llegada es [0, ∞), mide el concepto opuesto, es decir, el
grado de desacuerdo o incompatibilidad entre dos obje-
tos.
En la propuesta del algoritmo CLARABD de este traba-
jo, se usan funciones de distancia. Particularmente, las
distancias euclideana, manhattan y gower:
• Euclideana: es la distancia más usada y conocida, su fór-
mula de cálculo es:
• Manhattan: es usada generalmente en espacios discre-
tos (posiblemente innitos), su fórmula de cálculo es:
• Gower: usada cuando se dispone de tipos de datos mix-
tos (cualitativos y cuantitativos). Su forma de cálculo es:
donde s(A, B) es el coeciente de similaridad de Gower:
y p
1
es el número de variables cuantitativas continuas, p
2
es el número de variables binarias, p
3
es el número de va-
riables cualitativas (no binarias), r es el número de coin-
cidencias (1, 1) en las variables binarias, d es el número
de coincidencias (0, 0) en las variables binarias, α es el
número de coincidencias en las variables cualitativas (no
binarias) y G
h
es el rango (o recorrido) de la h-esima va-
riable cuantitativa [17].
Teniendo en cuenta estos elementos, se puede denir
un algoritmo de clasicación.
Denición 3 (Algoritmo de clasica-
ción). Un Algoritmo de Clasicación,
A, recibe como entrada un cubrimien-
to parcial y lo transforma en un cubri-
miento total.
A[(Ω, ℜ, δ, Q
1
, π
1
, f)] = (Ω, ℜ, δ, Q
2
, π
2
f)
Note que en el cubrimiento nal pue-
den aparecer modicados tanto el
conjunto de clases como la relación de
pertenencia. Además, en todo proceso
de clasicación se debe tener en cuen-
ta su principio fundamental: objetos
semejantes pertenecen a la misma clase;
objetos diferentes pertenecen a clases
distintas [14].
A partir del principio, es claro que lo
deseable es que la semejanza dentro del
grupo sea lo más alta posible. Es decir,
los grupos resultantes de un algo- ritmo
de clasicación deberían tener mayor
semejanza interior que exterior. La va-
rianza, que clásicamente es usada en es-
tadística, recoge la noción de semejanza
interior. Es decir, se desea obtener gru-
pos con la menor varianza posible.
Otro elemento importante al momento
de comparar objetos, es considerar el
caso en el que los objetos pertenezcan
a un espacio diferente de ℝ
n
. Por ejem-
plo, si se tiene los objetos O
1
= (dulce,
27, sábado, grande) y O
2
= (salado, 25,
jueves, mediano), no es posible usar la
distancia euclideana porque los espacios
contienen valores categóricos.
Note que la distancia de Gower si po-
dría abordar el problema, pero hay que
tener en cuenta ciertos elementos. A
continuación se usa este ejemplo para
ilustrar elementos de la denición 1. En
este caso, los objetos O
1
y O
2
tienen a
sabor, edad, día y tamaño como rasgos
descriptivos. Se sabe que cada rasgo

91
descriptivo tiene su propio dominio, en
este caso serían
• Dom(sabor) = {dulce, salado, agrio,
ácido}
• Dom(edad) = [0, 120] enteros
• Dom(día) = {lunes, martes, miércoles,
jueves, viernes, sábado, domingo}
• Dom(tamaño) = {pequeño, mediano,
grande}
Si bien la distancia eculideana no puede
ser usada en este caso, una forma gene-
ral de abordar este problema es notar
que los objetos O
1
y O
2
están en el mis-
mo espacio. Se puede proceder a com-
pararlos en cada rasgo usando funciones
auxiliares.
En este ejemplo se pueden denir cua-
tro funciones auxiliares, una para cada
rasgo: g
1
(dulce, salado), g
2
(27, 25), g
3
(-
sábado, jueves) y g
4
(grande, mediano).
Si todas las funciones g
i
(x, y), i = 1, 2,
3, 4 son de diferencia, entonces se tiene
diferencias parciales respecto a cada ras-
go descriptivo entre los objetos. Ahora,
para obtener una medida de diferencia
global, se deben combinar de alguna
manera las diferencias parciales. Espe-
cícamente, se puede usar la función de
distancia sintáctica.
Denición 4 (Distancia y semejanza
sintáctica). Sean A = (a
1
, a
2
, . . . , a
r
) y B =
(b
1
, b
2
, . . . , b
r
) dos objetos y g
i
(x, y), i =
1, . . . , r, funciones auxiliares, la distancia
sintáctica se dene como
En el mismo contexto, la semejanza sin-
táctica se dene como
donde α
i
=1 pondera la re-
levancia de cada rasgo.
La distancia sintáctica permite la com-
paración de objetos en cualquier espacio de representa-
ción e incluso ponderando la relevancia de cada rasgo
con el requisito de que las funciones auxiliares est´en
bien denidas. Note que la distancia de Gower ya per-
mite trabajar con datos mixtos, pero clara- mente la
aproximación al problema usando funciones auxiliares y
distancias sintácticas es todavía más general.
II. MATERIALES Y MÉTODOS
Como se puede apreciar, el MEC ofrece un marco gene-
ral para abordar el problema de clasicación. El algorit-
mo CLARABD de este trabajo es una extensión del algo-
ritmo CLARA. Su desarrollo se muestra en esta sección
y para ello se necesita presentar dos algoritmos que son
su insumo: K-medias y K-medoides.
K-medias
Por primera vez desarrollado por [18], el algoritmo k-me-
dias es quizá el Algoritmo de clasicación no jerárquica
más utilizado en toda la literatura. Sea en textos de con-
tenido teórico como [19, 20] o textos aplicados como [9,
21], siempre esta presente una sección dedicada al algo-
ritmo k-medias. A continuación se presenta el algoritmo.
El algoritmo recibe como entrada a un conjunto de obje-
tos en el espacio ℝ
n
y k (número de grupos a formar). El
resultado una partición del espacio de objetos, tal que,
optimiza la varianza global.
1. Calcular la Matriz Global de Distancias.
2. Seleccionar, los k objetos más alejados, como atractores
iniciales.
3. Calcular y almacenar la distancia entre cada objeto y
cada uno de los k atractores.
4. Particionar el espacio en grupos, asignando cada ob-
jeto al grupo del atractor más cercano.
5. Calcular, para cada grupo denido, su centroide.
6. Considerar los centroides recién calculados como
nuevos puntos atractores.
7. Regresar al paso (3).
8. Terminar cuando el conjunto de centroides sea idén-
tico que el de la iteración anterior.
K-medoides
Cabe señalar el algoritmo k-medoides es un método de
clasicación no supervisado. Un lector familiarizado
con el algoritmo k-medias encontrará grandes simili-
tudes. Siguiendo a [1], se presenta a continuación el
algoritmo.
V. Morales, B.Morales

92
ISSN 2477-9105 Número 22 Vol. 2 (2019)
1. Seleccionar una función de comparación entre ob-
jetos. Por ejemplo, si se trata de variables cualitativas se
suele usar la distancia euclideana, en este trabajo se usa
la distancia de Gower.
2. Calcular la Matriz Global de semejanza/diferencia,
esto es, la matriz de distancias.
3. Seleccionar, los k patrones más alejados, como atrac-
tores iniciales.
4. Calcular y almacenar la semejanza/diferencia entre
cada patrón y cada uno de los k objetos atractores
5. Particionar el espacio en grupos, asignando cada pa-
tron al grupo del atractor más cercano
6. Calcular, para cada grupo denido, su medoide
7. Considerar los medoides reci´en calculados como
nuevos patrones atractores.
8. Regresar al paso (4)
9. Terminar cuando el conjunto de medoides sea idén-
tico que el de la iteracion anterior.
La última partici´on obtenida, (idéntica a la de la itera-
ción anterior) es la respuesta nal del algoritmo. Con
el algoritmo k-medoides se tiene un mecanismo para
agrupar (por particionamiento) objetos en cualquier es-
pacio de representación. Por el hecho de calcular medoi-
des en lugar de centroides, el algoritmo k-medoides con-
verge más rápido a la única solución global posible en ese
espacio de representación y con ese conjunto de objetos.
CLARA
El algoritmo CLARA nace ante la necesidad de superar
las barreras de memoria y tiempo de cómputo del algo-
ritmo k-medoides (también conocido como Partitioning
Around Medoids PAM) y está claramente explicado en el
capítulo 3 de [1].
El método consiste, en términos generales, de dos pasos.
Primero, se obtiene una muestra de objetos de los cuales
se generan k grupos usando el algoritmo k-medoides.
Es decir, se tienen k objetos representativos (medoi- des)
de cada grupo. Segundo, cada objeto que no pertenece
a la muestra es asignado al objeto más cercano de los k
representativos. Esto resulta en una partición de todo el
conjunto de objetos.
En el segundo paso se calcula la distancia promedio entre
cada objeto de todos los datos y su objeto representativo.
Después de realizar este proceso varias veces (el valor por
defecto suele ser 5), se escoge la partición para la cual se
tiene la distancia promedio más baja. En términos más
especícos, los pasos del algoritmo CLARA son [22]:
1. Dividir aleatoriamente los conjuntos
de datos en múltiples subconjuntos con
tamaño jo.
2. Calcular el algoritmo PAM en cada
subconjunto y elegir los k objetos repre-
sentativos correspondientes (medoides).
Asignar cada observacion del conjunto
de datos completo al medoide más cer-
cano.
3. Calcular la media (o la suma) de las
diferencias de las observaciones con su
medoide más cercano. Esto se usa como
una medida de la bondad de la agrupa-
ción.
4. Retenga el subconjunto de datos para
el que la media (o suma) es mínima.
CLARABD
CLARABD es un algoritmo que tiene
dos objetivos. En primer lugar, extien-
de el algoritmo CLARA tal que pueda
usarse la distancia de Gower para obte-
ner la agrupación nal. Es decir, permi-
te usar datos mixtos (datos de tipo no-
minal, ordinal y binarios (a)simétricos).
K-medoides también puede usarse con
datos mixtos. Sin embargo, en el progra-
ma R existen limitaciones en su cálculo.
Actualmente existe un límite estricto,
el nu´mero de objetos debe ser menor
o igual a 65536. Cuando el número ob-
jetos supera este límite, se sugiere usar
el algoritmo CLARA. En este sentido,
el segundo punto en el que CLARABD
extiende a k-medoides en R es porque
permite realizar agrupaciones más allá
de 65536 objetos.
Especícamente, el punto 2 del algorit-
mo CLARA es adaptado en CLA- RABD.
Este paso del algoritmo en CLARABD
sería.
Con la opción de elegir la distancia de
Gower además de la euclídea y man-
hattan, se calcula el algoritmo PAM en
cada subconjunto y se eligen los k obje-
tos representativos correspondientes (me-
doides). Asignar cada observación del
conjunto de datos completo al medoide
93
más cercano.
Es decir, todas las disimilaridades re-
queridas por el algoritmo pueden ser
calculadas con la distancia de Gower.
El código del algoritmo CLARABD ha
sido plasmado en la función claraBD
y puede descargarse de https://github.
com/vmoprojs.
III. RESULTADOS
Simulacion
Para evaluar los resultados de CLA-
RABD, se ha congurado el siguiente
escenario de simulación. Se crearon 4
grupos de tamaño 100, un total de 400
objetos. Cada uno está compuesto de
dos atributos, una variable cuantitativa y
una nominal.
La variable cuantitativa fue construi-
da generando números aleatorios que
siguen una distribución normal con
distintas medias para cada grupo y va-
rianza constante. La variable categórica
fue construida mediante la generación
de números aleatorios con distribución
binomial con probabilidad
0,5. El código para reproducir los resul-
tados de la simulación se encuentra en
el apéndice A.
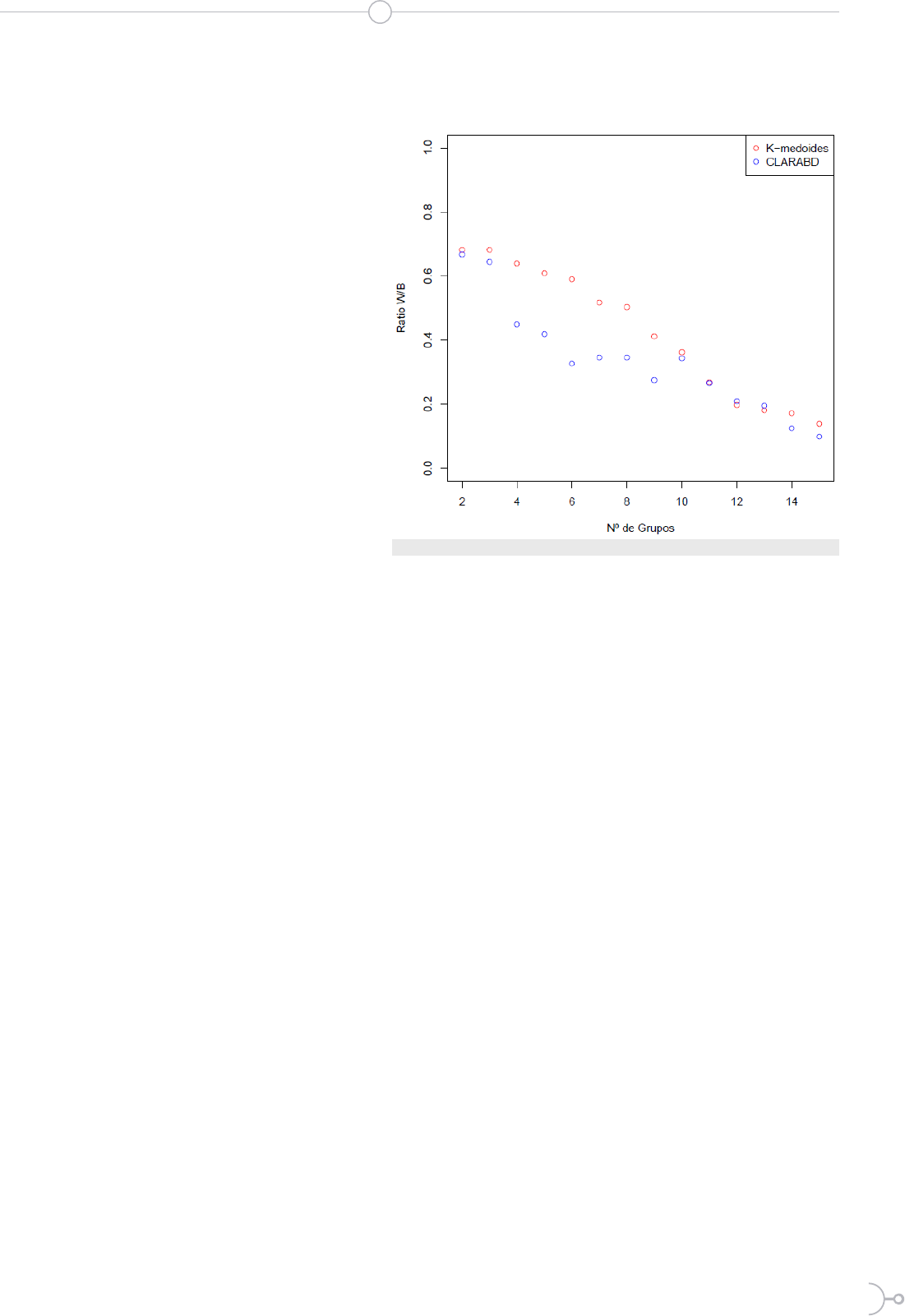
La gura 1 muestra el ratio within/
between para evaluar la consistencia
respecto al número de grupos. Efectiva-
mente, se observa que el ratio disminu-
ye a medida que aumenta el número de
grupos, lo que muestra consistencia en
la agrupacion. También se muestran los
valores para k-medoides como referen-
cia.
Se puede apreciar el ratio dentro (wi-
thin) y entre (between) la suma de cua-
drados tiene una caída signicativa en
4 grupos en CLARABD. K-medoides,
en contraste, decrece más lentamente.
Es posible que, al usar muestras de los
datos originales, CLARABD tiene más
probabilidad de capturar los cambios en estructura de la
agrupación a medida que aumenta el número de grupos.
Aplicación
A continuación se aplica el algoritmo CLARABD a un
conjunto de datos de crédito de un banco alemán. Estos
datos se obtuvieron del Repositorio de Aprendizaje Auto-
mático de la Universidad de California [23]. El conjunto
de datos, que contiene atributos y resultados sobre 1000
solicitudes de préstamo, fue proporcionado en 1994 por
el Profesor Dr. Hans Hofmann del Instituto de Estadística
y Econometría de la Universidad de Hamburgo. Ha ser-
vido como un importante conjunto de datos de prueba
para varios algoritmos de puntuación de crédito.
Una descripción más detallada de los datos puede en-
contrarse en el repositorio así como en la gura 5. Cuen-
ta con 21 en total (incluyendo el identicador de clien-
te), variables cuantitativas (duraci´on del crédito, monto,
edad, entre otros) y cualitativas (historial de crédito, des-
tino del crédito, si es extranjero, entre otras).
Los datos contienen una variable de incumplimiento de
crédito y, como un ejercicio de validación, se asume esta
variable como determinada por las demás variables del
conjunto de datos. Esto permite calcular una matriz de
confusión usando CLARABD y k-medoides.
La tabla 1 muestra los porcentajes respecto al total de
la matriz de con fusion. Su objetivo es mostrar que los
porcentajes son parecidos en la clasicación. Los valores
Figura 1: Ratio within/between vs nu´mero de grupos
V. Morales, B.Morales
94
ISSN 2477-9105 Número 22 Vol. 2 (2019)
sin paréntesis son los resultados de CLARABD y en pa-
réntesis estan los resultados de k-medodides. El apén-
dice B. contiene el codigo que reproduce los resultados
de la tabla 1.
Otra forma de comparar los resultados de los algoritmos
es a través de los representantes de los grupos y cuan se-
parados se encuentran. Los medoides que resultan de
CLARABD son los objetos 10 y 843, PAM tiene por me-
doides a 892 y 261.
La tabla 2 muestra estos resultados y se puede apre-
ciar que en algunas variables coinciden y en otras no. Por
ejemplo, en la variable ahorro se tiene exactamente el
mismo resultado, mientras que en la variable monto la
distancia es amplia entre los medoides. En general, exis-
ten diferencias en 12 de las 20 variables en ambos casos.
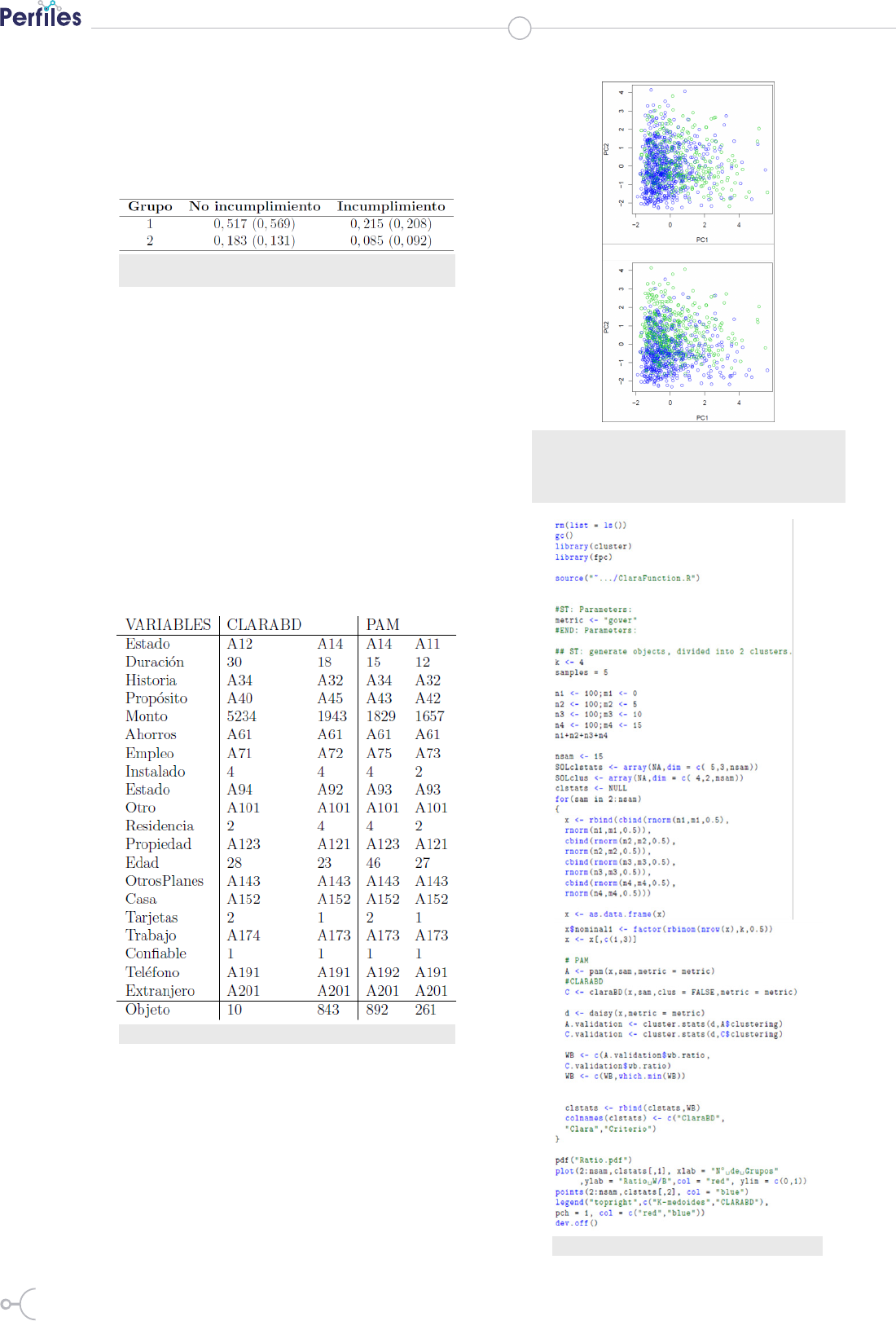
Finalmente, la gura 2 muestra un gráco biplot de las
variables numéricas. Este gráco utiliza las dos compo-
nentes más relevantes como resultado de aplicar un análi-
sis de componentes principales sobre las variables numé-
ricas. Ambas componentes representan el 44 % del total
de la varianza de los datos y se muestran las etiquetas de
la partición encontrada por los algoritmos CLARABD y
PAM. Se puede apreciar que los patrones de los conglo-
merados son similares.
Tabla 1: Matriz de confusion. CLARABD y en paréntesis k-me-
doides
Tabla 2: Centroides de cada partición, CLARABD y PAM.
Figura 2: Biplot de variables numéricas etiquetadas por las
agrupaciones de dos grupos resultantes. En el panel izquierdo
presenta el algoritmo CLARBD, en el lado derecho se presenta
el algoritmo PAM
Figura 3: código de simulación

95
Figura 4: código de aplicación
Figura 5: Descripción de los atributos de la aplicación
III. CONCLUSIONES
Se ha logrado extender el algoritmo
CLARA para datos mixtos. Para esto
se usa la distancia de gower dentro del
algoritmo CLARA tradicional. Los resultados de este
proceso se han plasmado desde una perspectiva de si-
mulación para evaluar la consistencia en la congura-
ción de las agrupaciones nales así como una aplicación
V. Morales, B.Morales

96
ISSN 2477-9105 Número 22 Vol. 2 (2019)
a datos reales. Ambos enfoques comparan los resultados
con k-medoides dado que este algoritmo permite usar la
distancia de gower.
Tanto el proceso de simulación como la aplicación a da-
tos reales muestran que CLARABD es consistente con
PAM, las agrupaciones son similares desde distintos en-
foques. En la simulación la consistencia se muestra a
través del ratio dentro/entre (within/between). La apli-
cación usa tres elementos para mostrar la consistencia
entre algoritmos.
En primer lugar, se presenta la matriz de confusión asu-
miendo la variable de incumplimiento como objetivo.
Luego se muestran las coincidencias que existen entre
los representantes (medoides) de los grupos obtenidos. Y,
nalmente, se muestra un gráco biplot donde los pa-
trones lucen muy parecidos. Todas estas aproximaciones
son evidencia de la coherencia del algoritmo propuesto:
CLARABD.
Existen puntos especícos de CLARABD que pueden ser
mejorados. Por ejemplo, por ahora, tanto la implemen-
tación de CLARA en R como la propuesta de CLARABD
usa muestreo aleatorio simple para obtener las muestras
del conjunto de objetos inicial. El diseño muestral podría
ocasionar cambios radicales en las agru-
paciones nales y responder de mejor
manera a un problema especíco. Por
ejemplo, si se podría plantear un mues-
treo estraticado que recoja de mejor
manera la probabilidad de selección y el
peso que tiene cada objeto.
CLARABD es funcional y puede traba-
jar con más allá del umbral actualmen-
te permitido por R (65536 objetos). No
obstante, el tiempo de cómputo aún es
un problema.
Tanto k-medoides como CLARA tienen
su código fuente programado en el len-
guaje C y R usa las funciones ejecutadas
en C. Esta es una práctica común en
R cuando se trata de procesos intensivos
en cómputo.
Un trabajo derivado del presente po-
dría implementar en C las rutinas más
exigentes. En particular, la asignación de
las observaciones no muestreadas a los
medoides más cercanos es exigente com-
putacionalmente.
R
eferencias
[1] Leonard Kaufman and Peter J Rousseeuw. Finding groups in data: an introduction to cluster
analysis, volume 344. John Wiley & Sons, 2009.
[2] Chris Fraley and Adrian E Raftery. How many clusters? which cluste- ring method? answers
via model-based cluster analysis. The computer journal, 41(8):578–588, 1998.
[3] Pedro Galeano and Daniel Pen˜a. Data science, big data and statistics. TEST, pages 1–41, 2019.
[4] Surekha Borra, Rohit Thanki, and Nilanjan Dey. Satellite Image Analy- sis: Clustering and
Classification. Springer, 2019.
[5] Brefeld Ulf, Jesse Davis, Jan Van Haaren, and Albrecht Zimmermann. Machine Learning and
Data Mining for Sports Analytics. Springer, 2019.
[6] Gautam K Vallabha, James L McClelland, Ferran Pons, Janet F Werker, and Shigeaki Amano.
Unsupervised learning of vowel categories from infant-directed speech. Proceedings of the Na-
tional Academy of Sciences, 104(33):13273–13278, 2007.
[7] Feng Zhen, Xiao Qin, Xinyue Ye, Honghu Sun, and Zhaxi Luosang. Analyzing urban de-
velopment patterns based on the flow analysis met- hod. Cities, 86:178–197, 2019.
[8] Martin Maechler, Peter Rousseeuw, Anja Struyf, Mia Hubert, and Kurt Hornik. cluster: Clus-
ter Analysis Basics and Extensions, 2017. R pac- kage version 2.0.6 — For new features, see the
’Changelog’ file (in the package source).
[9] Bater Makhabel. Learning data mining with R. Packt Publishing Ltd, 2015.
[10] R Core Team. R: A Language and Environment for Statistical Compu- ting. R Foundation
for Statistical Computing, Vienna, Austria, 2017. URL https://www.R-project.org/.
[11] Trevor Hastie, Robert Tibshirani, and Jerome Friedman. The elements of statistical learning,

97
V. Morales, B.Morales
ser, 2001.
[12] Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani. An introduction to
statistical learning, volume 112. Springer, 2013.
[13] Alan Julian Izenman. Modern multivariate statistical techniques. Regression, classification
and manifold learning, 2008.
[14] Salvador Godoy. Evaluacion de algoritmos de clasificacion basada en el modelo estructural de
cubrimientos. PhD thesis, Instituto Polit´ecnico Nacional, México, 5 2006.
[15] Liset Bandomo Toledo. Procedimiento para evaluar el nivel de comple- jidad de los procesos
de negocio a partir de su representacion grafica. PhD thesis, Universidad Central ?Marta Abreu?
de Las Villas, 2014.
[16] A Riquenes-Fernandez and E Alba-Cabrera. Collective classification: An useful alternative for
the classification of objects. In European Congress on Intelligent Techniques and Soft Computing
EUFIT, volume 97, pages 1875–1879, 1997.
[17] Amparo Baillo Moreno and Aurea Gran´e Ch´avez. 100 problemas re- sueltos de estad´ıstica
multivariante: (implementados en Matlab). Delta Publicaciones, Madrid, Espan˜a, 2008.
[18] J. MacQueen. Some methods for classification and analysis of multi- variate observations.
In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability,
Volume 1: Statistics, pages
281–297, Berkeley, Calif., 1967. University of California Press. URL https://projecteuclid.org/
euclid.bsmsp/1200512992.
[19] Brian D Ripley. Pattern recognition and neural networks. Cambridge university press,
2007.
[20] Rui Xu and Don Wunsch. Clustering, volume 10. John Wiley & Sons, 2008.
[21] Dan Toomey. R for Data Science. Packt Publishing Ltd, Unated King- dom, 1 edition, 2014.
[22] Alboukadel Kassambara. Statistical tools for high-throughput data analysis, 09 2018. URL
http://www.sthda.com/english/.
[23] Dua Dheeru and Efi Karra Taniskidou. UCI machine learning repository, 2017. URL http://
archive.ics.uci.edu/ml.