
20
ISSN 2477-9105 Número 23 Vol.1 (2020)
ANÁLISIS DE LA PREDICTIBILIDAD DE LAS CONCENTRACIONES
ANUALES DE PM2.5 EN QUITO, APLICANDO LA ENTROPÍA DE
KOLMOGÓROV-SINAI
Analysis the predictability of the annual concentrations of PM2.5 in Quito, applying the
entropy of Kolmogórov-Sinai
1
Marco-Vinicio Pino-Vallejo*,
2
Alfonso-Rodrigo Tierra-Criollo,
3
Nelly-Patricia Perugachi-Cahue-
ñas
1
Universidad Nacional de Chimborazo, Riobamba, Ecuador.
2
Universidad de las Fuerzas Armadas, Quito, Ecuador.
3
Escuela Superior Politécnica de Chimborazo ESPOCH, Riobamba, Ecuador.
*marcopinovallejo@hotmail.com
R
esumen
El material particulado de 2.5 micras conocido como PM2.5, se encuentran en el aire urbano, prin-
cipalmente debido a la contaminación vehicular. Los efectos en la salud son irreversibles debido a
que por su dimensión puede alojarse permanentemente en los alvéolos pulmonares. El objetivo de
la investigación fue analizar la predictibilidad de las concentraciones de PM2.5 en Quito-Ecuador
(0°13'12.46 "S, 78 ° 30'36.97" O, altura 2830 m), mediante la entropía de Kolmogórov-Sinai. Se uti-
lizaron los datos históricos de las concentraciones de PM2.5, registrados por la Red de Monitoreo
Atmosférico Metropolitano de Quito del período 2005-2016. Previo al análisis de predictibilidad se
calcularon los parámetros de tiempo de retardo, la dimensión de encaje y exponentes de Lyapunov
que determinan la dinámica del sistema, para procesar los datos se usa el modelo Tisian. El mayor
número de exponentes positivos de Lyapunov se encuentran en los años 2011, 2013 y 2016. La en-
tropía de Kolmogórov-Sinai tiene una tendencia a incrementarse en el transcurso de los 12 años
analizados, lo cual implica una disminución en la predictibilidad de los datos de PM2.5, debido a
la pérdida de información a lo largo de la evolución del sistema.
Palabras Claves: Material Particulado PM2.5, Tiempo de Retardo, Dimensión de Encaje, Expo-
nentes de Lyapunov, Entropía de Kolmogórov-Sinai
A
bstract
The particulate material of 2.5 microns known as PM2.5 is found in urban air, mainly due to
vehicular contamination. The health effects are irreversible because by their size it can permanently
lodge in the pulmonary alveoli. The objective of the research was to analyze the predictability of
PM2.5 concentrations in Quito-Ecuador (0-13'12.46"S, 78'30'36.97" O, height 2830 m), using the
entropy of Kolmogórov-Sinai. The historical data of the concentrations of PM2.5, recorded by the
Quito Metropolitan Atmospheric Monitoring Network from 2005-2016, were used. Prior to the
predictivity analysis, the time delay parameters, the fit dimension and the Lyapunov exponents
that determine the system dynamics, were calculated. The Tisian model is used to process the
data. The largest number of positive exponents of Lyapunov are found in 2011, 2013 and 2016.
Kolmogorov-Sinai entropy has a tendency to increase over the course of the 12 years analyzed,
which implies a decrease in the predictability of PM2.5 data, due to the loss of information over the
course of the system evolution.
Keywords: PM2.5 Particulate Material, Delay Time, Lace Dimension, Lyapunov Exponents,
Kolmogórov-Sinai Entropy
Fecha de recepción: 03-10-2018 Fecha de aceptación: 23-12-2019

21
I. INTRODUCCIÓN
El material particulado de 2.5 micras (PM2.5),
conocido como polvo en suspensión es respirable
debido a su dimensión aerodinámica y al ingresar
al sistema respiratorio puede alojarse permanen-
temente en los alvéolos pulmonares con efectos
adversos para la salud (1). Este contaminante at-
mosférico se origina a partir de la combustión de
combustibles fósiles, procesos industriales, agricul-
tura, construcción de carreteras, procesos erosivos
y la extracción de material pétreo (2). En la atmós-
fera urbana el 70% y 80% de PM2.5, se origina por
el tráfico vehicular (3). El valor fijado por la Organi-
zación de la Salud para concentraciones anuales de
PM2.5 es de 10 μg/m3. El resultado del estudio de
calidad del aire realizado entre el 2016 en el Distrito
Metropolitano de Quito supera las normas nacio-
nales y de la OMS (4).
El control de la contaminación por PM2.5 pasa por
diferentes etapas, desde las normativas, políticas,
educativas y técnico científicas, cuya efectividad
de pende de su cumplimiento y avance tecnológi-
co-científico, lamentablemente desde el punto de
vista científico presenta grandes dificultades por
ser un sistema complejo, impredecible y aparen-
temente caótico (5). Los especialistas en dinámica
no lineal usan la palabra “caos” como un término
técnico con un significado matemático preciso para
definir un comportamiento irregular e impredeci-
ble de un sistema que es determinístico y no lineal
(6,7).
Desde el descubrimiento de la impredecibilidad en
los sistemas determinísticos, los cuales conllevaron
al estudio de sistemas dinámicos, muchos trabajos
de investigación fueron desarrollados para encon-
trar las propiedades del caos con los cuales poder
clasificar estos sistemas (8,9). Por ejemplo, indica-
dores dinámicos como la sensibilidad a las con-
diciones iniciales, los exponentes de Lyapunov, la
entropía de Kolmogorv-Sinai, entre otros, fueron
desarrollados para hacer una caracterización más
precisa de estos sistemas (10,11).
Así por ejemplo, aparecen los denominados “sis-
temas-K” que exhiben una propiedad matemática
conocida como “mezcla”, es decir una entropía de
Kolmogorv-Sinai positiva. Esto significa que los sis-
temas en cuestión son extremadamente sensibles a
las condiciones iniciales, de modo que dos trayec-
torias inicialmente próximas divergen según una
tasa exponencial. Esta tasa es medida por los expo-
nentes de Lyapunov, que son equivalentes a la en-
tropía de Kolmogorv-Sinai y pueden ser fácilmente
calculados, para establecer el grado de coticidad y la
factibilidad de que puedan ser predichos (12).
Con estos antecedentes el objetivo de la investiga-
ción es analizar el grado de predictibilidad de las
concentraciones de PM2.5 del período 2005-2016
monitoreados en Quito-Ecuador, mediante siste-
mas dinámicos no lineales en base a la entropía de
Kolmogórov-Sinai (13).
II. MATERIALES Y MÉTODOS
Para el análisis de las concentraciones de material
particulado PM2.5 del período 2005-2016 en Qui-
to-Ecuador, se utilizaron los datos históricos de las
registrados Red de Monitoreo Atmosférico Metro-
politano de Quito. Para el análisis no lineal se apli-
có los programas del modelo Tisean v.2.0 (13).
Para la reducción del ruido se utilizó el programa
nrlazy, para calcular el Tiempo de Retardo se utili-
zó el programa mutual, para la dimensión de encaje
el programa false neighbors y para los Exponentes
de Lyapunov el programa lyap_spec. Para el análi-
sis de la entropía Kolmogórov-Sinai se sumaron los
exponentes positivos de Lyapunov de cada año.
Reducción del ruido
El estudio de series de datos puede llevar a sa-
car conclusiones erróneas ya que los datos que se
toman como magnitud de la variable a analizar
suelen estar influidas por varios factores que intro-
ducen distorsiones a las que se denomina ruido y
por lo tanto no permiten observar con claridad los
patrones dinámicos que se quiere analizar (14). El
algoritmo no lineal más simple para la reducción de
ruido consiste en reemplazar la coordenada central
de cada vector de encaje, por un promedio local de
esta coordenada, como se expresa en la ecuación 1:
(1)
Al escoger una m dimensión de encaje y un ade-
Pino, Tierra, Perugachi

22
ISSN 2477-9105 Número 23 Vol.1 (2020)
cuado tiempo de retardo τ, por cada vector de en-
caje S
n
se forma una vecindad U
n
e
, se forma en el
espacio de fase que contiene todos los puntos S
n
tal
que ||S
n
–S´|| < , donde es el radio de la vecindad,
que debe ser lo suficientemente grande para cubrir
la extensión de ruido y S´ el espacio de fase inicial
(15). Por cada vector de encaje S
n
= (S
n-(m-1)
,....S
n
) con
λ=1, la coordenada corregida es S
n-(m/2)
, se calcula
como el promedio sobre la vecindad U
n
e
.
Tiempo de Retardo
El tiempo de retardo, es el paso más importante en
el análisis del espacio de fases, es la técnica de re-
construcción del sistema, formando vectores y eje-
cutando una proyección en el espacio de fases, que
es un espacio físico que permite detectar variables
dinámicas, en este método se busca la relación biu-
nívoca de los datos en el espacio de las fases (16).
El método de reconstrucción de espacio de fase más
importante es el método de retardo. Los vectores en
un nuevo espacio, el espacio de empotramiento, se
forman a partir de los valores retardados de las me-
diciones escalares expresado en la ecuación 2:
(2)
El número m de elementos se denomina dimensión
de retardo, el tiempo τ se denomina generalmente
retardo. Los teoremas incorporados por Takens (17)
y por Sauer, Yorke and Casdagli, concluyen que Sn
son mediciones escalares del estado de un sistema
dinámico, entonces bajo este criterio, la incorpora-
ción de retardo de tiempo proporciona una imagen
uno a uno del conjunto original x siempre que m
sea lo suficientemente grande. Si N mediciones es-
calares están disponibles, el número de vectores de
inclusión se estima que será N-(m-1)τ. (18)
Dimensión de Encaje
La idea del algoritmo del falso vecino es que para
cada punto Ṧ
i
en la serie de tiempo busque su vecino
más cercano Ṧ
j
en un espacio m-dimensional. Por
lo tanto calcula la distancia ||Ṧ
i
- Ṧ
j
||, que reincide en
ambos puntos. Como se expresa en la ecuación 3:
(3)
Al exceder Si un umbral heurístico determinado St,
este punto está marcado como un vecino falso ve-
cino (18). El criterio de que la dimensión de encaje
es lo suficientemente alta, es la fracción de puntos
para la cual Si > St es cero, o al menos suficiente-
mente pequeño. Si la relación de la distancia de la
interacción y del vecino más cercano excede a un
valor determinado, el punto se marca como un ve-
cino equivocado. (19)
Exponentes de Lyapunov
El cálculo del espectro completo de Lyapunov re-
quiere considerablemente más esfuerzo que el ex-
ponente máximo (20). El proceso consiste en una
estimación de los Jacobianos locales, es decir, de la
dinámica linealizada que gobierna el crecimiento
de las perturbaciones infinitesimales. El caos surge
del crecimiento exponencial de las perturbaciones
infinitesimales es así que para garantizar el análisis
de esta inestabilidad están los exponentes de Lyapu-
nov, que cuantifican el momento que dos trayecto-
rias se alejan, como se expresa en la ecuación 4:
(4)
Donde: r(t) es el semi-eje mayor de una elipse, r es
el radio pequeño y t es el tiempo grande, en general
se establece λ
1
≥ λ
2
………λ
d
. En un sistema caótico
al menos un exponente de Lypunov es positivo. (21)
Entropía de Kolmogórov-Sinai
Este tipo de entropía también llamada métrica (h),
mide la pérdida de información a lo largo de la evo-
lución del sistema. Como se expresa en la ecuación
6, este tipo de entropía es determinada por la suma
de exponentes positivos de Lyapunov (22,23). Tiene
importante significado cuando se aplica a sistemas
de los cuales no se dispone más que de series tem-
porales de valores de determinada variable.
(5)
Este tipo de entropía se relaciona con la previsibi-
lidad que expresa una escala de tiempo promedio
hasta la cual las predicciones pueden ser posibles
(24). Esta cantidad invariante intrínseca del sistema
tiene una relevancia singular para la caracterización
de la previsibilidad (25). Los valores más altos de h
23
implican valores más bajos de la predictibilidad 1/h,
es decir, cuanto más caótico, menos predecible.
III. RESULTADOS
A continuación se exponen los resultados del proce-
samiento las series de datos anuales de las concen-
traciones de PM2.5 dentro del período 2005-2016.
Años Tiempo de Retardo Dimensión de Encaje
2005 9 8
2006 9 7
2007 8 7
2008 9 9
2009 10 6
2010 9 10
2011 10 12
2012 10 7
2013 9 15
2014 9 11
2015 10 7
2016 9 16
Tabla 1. Tiempo de Retardo y Dimensión de Encaje
En la Tabla 1, se indican los valores del Tiempo
de Retardo que representan los primeros míni-
mos de la función de correlación mutual infor-
matión, en el espacio de las fases, además de los
valores de la Dimensión de Encaje que usa la
función false neighbors, en la cual debe ser cero
su valor para tener el valor óptimo de dicha di-
mensión (11), estos resultados permiten recons-
truir la serie de datos en el espacio de las fases y
determinar los coecientes de Lyapunov.
Años
Exponentes de Lyapuvov
1 2 3 4 5 6
2005 0.0102 0.0043
2006 0.0102 0.0034
2007 0.0076 0.0015
2008 0.0064 0.0025
2009 0.0082 0.0011
2010 0.0081 0.0044 0.0009
2011 0.0072 0.0048 0.0024 0.0001
2012 0.0086 0.0023
2013 0.0103 0.0074 0.0053 0.0033 0.0015
2014 0.0081 0.0045 0.0018
2015 0.0077 0.0018
2016 0.0115 0.0081 0.0060 0.0042 0.0025 0.0004
Tabla 2. Exponentes positivos de Lyapuvov
En la Tabla 2, se observan los resultados de los cál-
culos de los exponentes de Lyapunov positivos en-
contrados en la serie de datos, que permiten esta-
blecer que es un sistema hipercaótico.
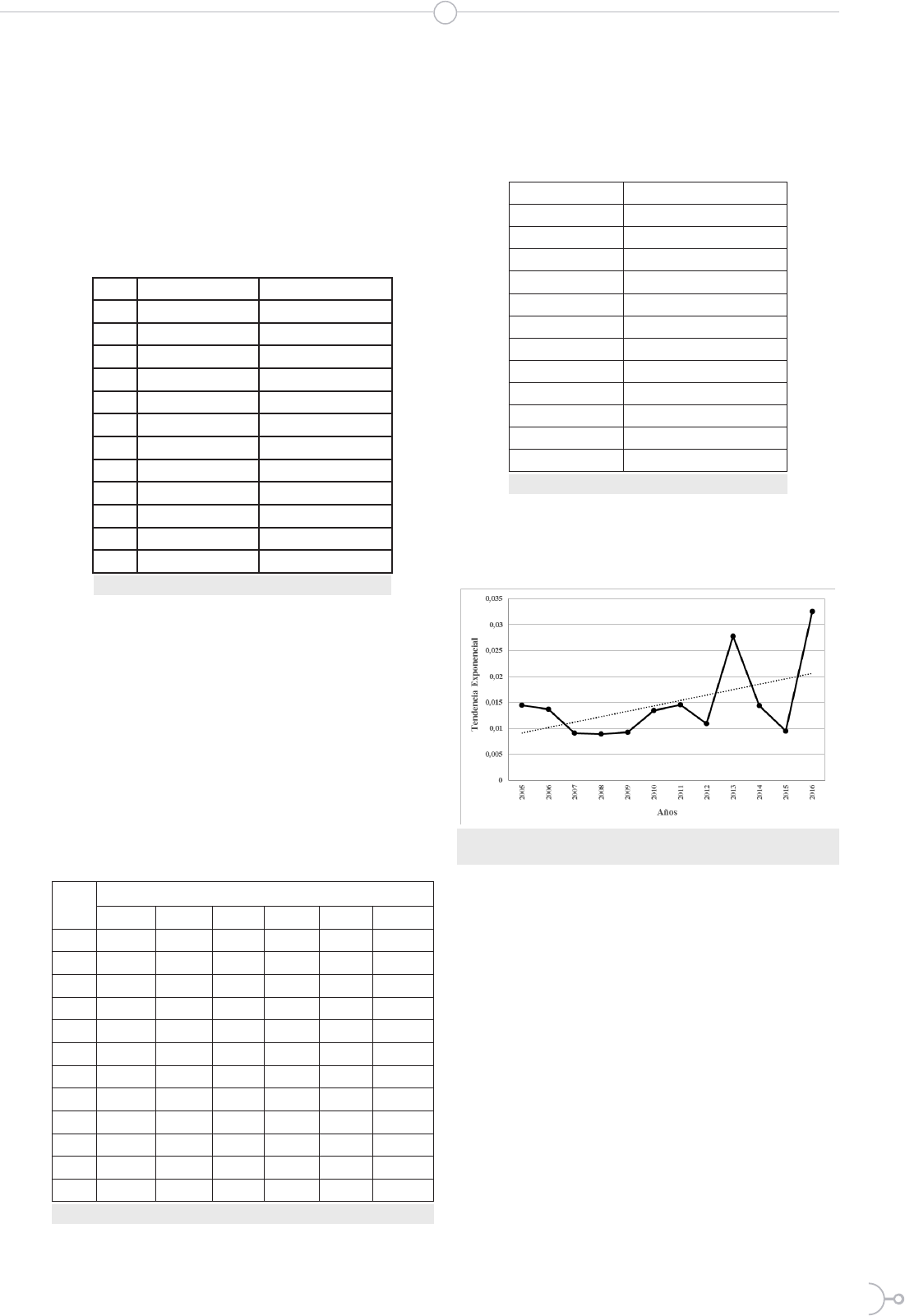
Años Entropia K-S
2005 0.0145
2006 0.0137
2007 0.0091
2008 0.0089
2009 0.0093
2010 0.0134
2011 0.0146
2012 0.0109
2013 0.0278
2014 0.0144
2015 0.0095
2016 0.0326
Tabla 3. Entropía de Kolmogórov-Sinai
En la Tabla 3, se encuentran la sumatoria de los ex-
ponentes de Lyapunov positivos que conforman los
valores de la Entropía Kolmogórov-Sinai (K-S).
Figura 1. Entropía de Kolmogórov-Sinai para las concentraciones anuales
de PM2.5 del período 2005 - 2016
En la Figura 1 de la Tabla 3, se puede observar
una tendencia aumentar de la entropía de Kolmo-
górov-Sinai.
IV. DISCUSIÓN
En el procesamiento de las series de datos anuales
de las concentraciones de PM2.5 dentro del perío-
do 2005-2016, se identifican variaciones significa-
tivas a partir del año 2010 tanto en los valores que
constituyen la reconstrucción de los datos en un
espacio multidimensional que determinan el Tiem-
po de Retención como en la dimensión mínima en
el espacio de las fases referentes a la Dimensión de
Encaje.
Pino, Tierra, Perugachi

24
ISSN 2477-9105 Número 23 Vol.1 (2020)
El número de exponentes positivos de Lyapunov,
demuestran que existen perturbaciones infinite-
simales en las series de datos de las concentracio-
nes anuales de PM2.5, cuya sumatoria establece
una tendencia creciente a partir del año 2010 que
se incrementa drásticamente en los años 2011, 2013
y 2016, dentro el principio de la entropía de Kol-
mogórov-Sinai estos valores se interpretan como la
pérdida de información en la serie de datos, que a
medida que se incrementan dificultan más la pre-
dictibilidad del sistema usando la teoría del caos.
V. CONCLUSIONES
El número de exponentes de Lyapunov, establecen
en promedio una dinámica hipercaótica, al presen-
tar más de un coeficiente positivo en los 12 años
analizados.
La tendencia de los valores que representan la en-
tropía de Kolmogórov-Sinai es creciente, por lo que
se determinan que la predictibilidad para las con-
centraciones anuales de PM2.5 es cada vez menos
probable usando la teoría del caos, debido a la pér-
dida de información del sistema en el tiempo.
R
eferencias
1. Linares Cristina, Díaz Julio. Efecto de las partículas de diámetro inferior a 2,5 micras (PM2,5) sobre los
ingresos hospitalarios en niños menores de 10 años en Madrid. Gac Sanit. 2009; 23(3): 192-197. Disponible
en: http://scielo.isciii.es/ scielo.php?script=sci_arttext&pid=S0213-91112009000300005&lng=es.
2. Rojas Bracho, Leonora; Garibay Bravo, Verónica Las partículas suspendidas, aeropartículas o aerosoles:
¿hacen daño a la salud?; ¿podemos hacer algo? Gaceta Ecológica, núm. 69, octubre-diciembre, 2003, pp.
29-44.
3. Ballester, F; Querol, X and Medina, S. Situación actual, prioridades de actuación y necesidades de inves-
tigación en contaminación atmosférica y salud en España: conclusiones del taller AIRNET de Barcelona.
Gac Sanit. 2007; (2007), 21:70-5.
4. Secretaría del Ambiente, Informe de calidad del aire en el Distrito Metropolitano de Quito 2016, acceso
3 de junio de 2019, http://www.quitoambiente.gob.ec/ambiente/ images/Secretaria_Ambiente/red_moni-
toreo/informacion/ICA2016.pdf.
5. Chuquer, David & Ampudia Vásquez, Santiago & Cruz, Carolina & Bustamante, Leonardo & Ramirez
Cevallos, Francisco & reina, carlos. (2018). Contaminación del aire a lo de calle en quito, caso estudio
Guayaquil y Espejo, Revista Perles. 2. 90-99.
6. Alligood, K; Sauer, T and Yorke, J., Chaos an introduction to dynamical systems. New York, Springer-Ver-
lag, 1996.
7. Hilborn, R.C., Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers. Oxford
University Press, New York, Oxford, 1994.
8. Hegger, R; Kantz, H and Schreiber, T. Practical implementation of nonlinear time series methods: e
TISEAN package, Chaos, 1999, 9, 413; https://doi.org/10.1063/1.166424.
9. Escudero I. y Haro A., “Modelación y pronóstico del potencial energético hídrico del río Blanco del
cantón Riobamba usando la teoría del caos y un método convencional”, Rev. XVI Jornadas de estadística e
informática, Guayaquil, Ecuador, 2010.
10. Garín F. Janampa A., Juan M. Pesantes R. y Martín B. Sandoval C., Generalization of the kolmogorov-si-
nai entropy: z-logistic maps, Anales Cientícos, 2015, 76, 237-240
11. Da- Hai Xia et al., Atmospheric corrosion assessed from corrosion images using fuzzy Kolmogorov–Si-
nai entropy, Corrosion Science, 2017, 120, 251-256.
12. Das, Moupriya and Costa, Anthony B. and Green, Jason R, Extensivity and additivity of the Kolmogo-
rov-Sinai entropy for simple uids, American Physical Society, Phys. Rev., 2017, E 95, 022102.
13. Pinos M., “Estimación del cambio climático en la ciudad de Riobamba usando la teoría del caos”, Tesis
de pregrado, Universidad Nacional de Chimborazo, Ecuador, 2002.
14. Fraedrich, K., Estimating weather and climate predictability on attractors. Journal of the Atmospheric
Sciences, 1987, 44, 722-728.
15. Fernández, D. Reducción del ruido y predicción de series temporales de alta frecuencia mediante sis-
temas dinámicos no lineales y técnicas neurales. Banco Nacional de Uruguay. Disponible en 2014. http://
www.bvrie.gub.uy/ local/File/doctrab/2014/1.2014.pdf.
16. Kennel, M, Brown, R and Abarbanel,H, Determining embedding dimension for phase-space recons-
truction using a geometrical construction. Phys. Rev., 1992. A 45, 3403.

25
17. Sauer, T; Yorke, J and Casdagli, M., Embedology, J. Stat. Phys. 1991, 65, 579.
18. Takens, F., Detecting strage attractors in turbulence, Lecture notes in Math. v.898, Springer-Verlag, New
York, pp. 366-381, 1981.
19. Bejar J., Caracterización de datos electrocardiográcos mediante la teoría del caos, Informe nal conve-
nio ESPOCH-FUNDACYT, Riobamba, Ecuador, 2001.
20. Taher A. zar and Vaidyanathan S., Advances in Chaos eory and Intelligent Control, Springer Interna-
tional Publishing Switzerland 2016.
21. Ruelle D., “Early chaos theory”, Physics Today, pp. 27, May, 2013.
22. Inga Stolz, and Karsten Keller, Tom Meyerovitch, Sieye Ryu, A general symbolic approach to Kolmogo-
rov-Sinai entropy, Entropy 2017, 19, 675.
23. Santos Burguete C., “Física del caos en Predicción Meteorológica. Edi. Digital AEMET, 2018.
24. Haro, A., Llosas Y., Lamaico C., Predicción de datos meteorológicos en cortos intervalos de tiempo en la
ciudad de Riobamba usando la Teoría del Caos. Sistemas Cibernética e Informática, 2016, 13, 35:41.
25. Van Beijeren, H. and Dorfman, J. R. and Posch, H. A. and Dellago, Ch., Kolmogorov-Sinai entropy for
dilute gases in equilibrium. American Physical Society, 1997, 5272—5277.
Pino, Tierra, Perugachi