
20
ISSN 2477-9105 Número 24 Vol.1 (2020)
SMOTEMD: UN ALGORITMO DE BALANCEO DE DATOS MIXTOS PARA
BIG DATA EN R.
SMOTEMD: a mixed data balancing algorithm for Big Data in R.
1
Víctor Morales-Oñate*,
2
Luis Moreta,
3
Bolívar Morales-Oñate
1
Banco Solidario, Riesgos, Analítica de Datos, Quito, Ecuador.
2
Escuela Politécnica Nacional, Facultad de Ciencias, Departamento de Economía Cuantitativa,
Quito, Ecuador.
3
Escuela Superior Politécnica de Chimborazo, Facultad de Ciencias, Ingeniería Química/Grupo de
investigación Data Science Research Group, Riobamba, Ecuador.
*victor.morales@uv.cl
R
esumen
Analizar muestras con datos desbalanceados es un desafío para quien debe utilizarlos en términos
de modelización. Un contexto en el que esto sucede es cuando la variable de respuesta es binaria y
una de sus clases es muy pequeña en proporción respecto al total. Para la modelización de variables
binarias se suele usar modelos de probabilidad como logit o probit. No obstante, estos modelos pre-
sentan problemas cuando la muestra no es balanceada y se desea elaborar la matriz de confusión de
donde se evalúa el poder predictivo del modelo. Una técnica que permite balancear los datos obser-
vados es el algoritmo SMOTE, el cual trabaja con datos numéricos exclusivamente. Este trabajo es
una extensión de SMOTE tal que permite el uso de datos mixtos (numéricos y categóricos). Al usar
datos mixtos, la presente propuesta también permite superar la barrera de 65536 observaciones que
tiene el software R cuando trabaja con distancias de datos categóricos. Mediante un estudio de si-
mulación, se logra verificar las bondades del algoritmo propuesto: SMOTEMD para datos mixtos.
Palabras Claves: SMOTE, Clasificación, Muestras desbalanceadas
A
bstract
Analyzing samples with unbalanced data is a challenge for those who should use them in terms of
modeling. A context in which this happens is when the response variable is binary and one of its
classes is very small in proportion to the total. For the modeling of binary variables, probability
models such as logit or probit are usually used. However, these models present problems when
the sample is not balanced and it is desired to elaborate the confusion matrix from which the
predictive power of the model is evaluated. One technique that allows the observed data to be
balanced is the SMOTE algorithm, which works with numerical data exclusively. This work is an
extension of SMOTE such that it allows the use of mixed data (numerical and categorical). By using
mixed data, this proposal also makes it possible to overcome the barrier of 65536 observations that
the R software has when working with categorical data distances. Through a simulation study, it is
possible to verify the benefits of the proposed algorithm: SMOTEMD for mixed data.
Keywords: SMOTE, Classification, Unbalanced samples.
Fecha de recepción: 18-01-2020 Fecha de aceptación: 31-03-2020 Fecha de publicación: 24-04-2020
I. INTRODUCCIÓN
En ocasiones el investigador se enfrenta a situacio-
nes donde la variable dependiente es observada con
muy poca frecuencia como, por ejemplo, en el caso
de fraudes bancarios (1), análisis de resultados de
ecosistemas donde habita fauna en peligro de ex-
tinción (2) o el análisis de países en conflicto (3). El
conjunto de datos que se utiliza en este contexto se
le conoce como datos desbalanceados (4).

21
Existen diversos campos en los que los eventos de
poca frecuencia (raros) o datos desbalanceados
tienen gran relevancia, no solo por el evento en sí
mismo, sino también por el alto costo que puede
implicar el equivocarse en su predicción (5). Den-
tro de este marco, cuando se realiza un modelo de
predicción con variable de respuesta binaria como
la regresión logística, autores como (3) muestran
que existe una distorsión en la probabilidad de que
ocurra el evento raro dado un vector de caracterís-
ticas, es decir que Pr(Y
i
=1|x
i
)=π
i
será generalmente
menor para los eventos raros, por tanto π
i
(1-x
i
) de
igual manera es más pequeño para los eventos raros
y la varianza es mucho mayor.
Por otro lado autores como (6) mencionan que en
los modelos de predicción con eventos raros exis-
te un alto grado de error en las clases minoritarias.
En virtud de que estas clases son relativamente pe-
queñas, entonces la afectación en ciertos criterios
de evaluación como la precisión o exactitud es in-
adecuada. Por ejemplo, si tomamos el caso de una
muestra desbalanceada en donde existe un total de
98% de casos donde la variable dependiente es igual
a cero y 2% de los casos son iguales a uno (clase mi-
noritaria), cuando el modelo predice a todos los ca-
sos que son igual a cero, entonces tendría una exac-
titud del 98%. En principio parece ser una exactitud
alta, sin embargo, el total de los casos raros están
mal clasificados. Es por esto que también se utiliza
una evaluación distinta de los diferentes modelos
como la Curva ROC y su área bajo la curva AUC
(7). La curva ROC se forma al graficar la Tasa de
Verdaderos Positivos (TPR = verdaderos positivos /
positivos) contra la Tasa de Falsos Positivos (FPR=
falsos positivos / positivos). Por ejemplo, si tenemos
10 individuos en una muestra donde 9 de ellos son
positivos y 1 es negativo, entonces TPR=1 y FPR = 1.
Esto representa un par ordenado sobre la diagonal
indicando una mala clasificación debido a la mues-
tra desbalanceada.
Al identificarse las distorsiones que pueden conlle-
var una muestra desbalanceada para modelos de
predicción como Logit, se han generado alternati-
vas que tratan de solucionar estos problemas, estas
soluciones abordan el desbalance desde diferentes
visiones.
Muchas alternativas se han presentado con respecto
a las muestras desbalanceadas y una de las pioneras
en buscar una solución a este problema es SMOTE
(Synthetic Minority Over-sampling Technique) (6),
donde se combinan enfoques de sobre-muestreo y
sub-muestreo. No obstante, han surgido diferentes
variantes de SMOTE que buscan mejorar el rendi-
miento de este algoritmo desde distintos puntos de
vista y modificaciones. Una de estas propuestas es la
de (8) donde el algoritmo ADASYN (Adaptive Syn-
thetic) utiliza una distribución no uniforme para la
creación de individuos sintéticos de la clase minori-
taria en función de la proporción del número de ve-
cinos cercanos que encuentra por individuo. Otro
enfoque para tratar de contrarrestar los efectos de
los datos desbalanceados son las matrices de costo,
es decir, ponderar los costos de predecir mal una
clase. El trabajo de (9) analiza este punto de vista
basándose en técnicas de curvas de costo donde se
modifica el sobre-muestreo y el sub-muestreo con
algoritmos de aprendizaje basados en un árbol de
decisión.
SMOTE: Synthetic Minority Over-sampling Te-
chnique
Cuando se trabaja con muestras en el que la falta
de datos de interés clasificados con uno es escasa se
dificulta la detección de regularidades dentro de los
casos raros (clase minoritaria) (6). Es por esto que
en (10) se propone una metodología que combina el
sobre-muestreo y el sub-muestreo de las diferentes
clases. SMOTE es un algoritmo donde lo que pri-
ma es la creación de individuos sintéticos a partir
de individuos de la clase minoritaria. Esto se realiza
determinando, en primera instancia, una vecindad
entre los individuos cercanos. Un nuevo individuo
es creado al tomar la distancia entre los individuos
de la misma vecindad y esta distancia se multipli-
ca por un valor aleatorio entre 0 y 1. Por un lado,
como resultado se obtiene una clase minoritaria
aumentada dependiendo el número de individuos
sintéticos que se escoja aumentar por cada indivi-
duo observado. Por otro lado, se puede sub mues-
trear a la clase mayoritaria de forma que se escoge
una muestra aleatoria menor de esta clase lo que a
la final equilibra las proporciones de las diferentes
clases y así se eliminan las distorsiones por el no ba-
lanceo de las clases.
El algoritmo de SMOTE ha demostrado tener un
mejor rendimiento medido con el indicador de la
Morales, Moreta, Morales

22
ISSN 2477-9105 Número 24 Vol.1 (2020)
curva ROC y el área bajo la curva AUC con res-
pecto a la multiplicación aleatoria de los individuos
de la clase minoritaria. Esto debido a que entre sus
ventajas se destaca el que permite hacer que el clasi-
ficador construya regiones de decisión más grandes
que contienen puntos cercanos de la clase minori-
taria. Esto facilita al modelo crear regiones de deci-
sión más amplias, esto conlleva a una mayor cober-
tura de la clase minoritaria (10).
Corrección previa.
Dentro del análisis de eventos raros para modelos
logit, en (3) se menciona la corrección de previa.
Aquí se aborda a las muestras desbalanceadas des-
de un enfoque post estimación. Los autores men-
cionan una corrección del término constante en
donde se calcula un nuevo β
0
en función de la pro-
porción de la clase minoritaria τ y el promedio del
y ȳ estimado (11). La correción de la constante se
muestra en la ecuación (1):
(1)
Una de las ventajas de la implementación de esta
corrección es la facilidad de implementación. Ade-
más, todos sus parámetros pueden ser calculados
de forma sencilla. Sin embargo, se ha mostrado que
en caso de que no exista una correcta especificación
en el modelo los estimadores β
i
son menos robustos
(12).
Enfoque al Big Data.
En la actualidad las mejoras tecnológicas en in-
fraestructura y la reducción de los costos de reco-
lección de datos han permitido que se puedan ge-
nerar bases con un gran número de datos (13). La
minería de datos se genera en diferentes sitios cada
día como es el caso de Redes Sociales (14) o Centro
Meteorológicos (15). Por lo tanto, muchos investi-
gadores están trabajando en la creación de nuevos
y mejores algoritmos de agrupamiento que buscan
manejar datos más complejos y extensos en que se
reduzca el costo computacional y por tanto aumen-
tar la escalabilidad y la velocidad de procesamiento
(16).
Los problemas de datos desbalanceados también
pueden afectar a las grandes bases de datos, y por
tanto la aplicación de técnicas estadísticas puede
ser desafiante (17). No obstante, el problema puede
no solo presentarse por el costo computacional sino
también por la naturaleza del problema que causa
el desbalance. Esto se plantea en (18) donde se men-
ciona que en las futuras investigaciones sobre datos
desbalanceados se deberá tener en cuenta el abor-
dar el problema de Big Data y a su vez la descom-
posición de múltiples clases. Para el problema mul-
ticlase, en (19) proponen usar diferentes esquemas
de binarización y ad-hoc, pero esto puede limitar el
panorama multiclase.
Como se ha mencionado, el algoritmo SMOTE uti-
liza un tipo de clustering que busca los k vecinos
más cercanos (KNN) entre los individuos de la clase
minoritaria (20). En (21) se menciona que SMOTE
es uno de los algoritmos más populares para abor-
dar las bases de datos desbalanceadas. La lógica de
elaborar clusters con KNN utiliza la distancia eucli-
diana, la cual no trabaja con variables categóricas.
Es por esto que este trabajo presenta una alternati-
va para trabajar con variables mixtas (cuantitativas
y cualitativas) y también con un volumen grande
de datos. En (22) se presenta un algoritmo llamado
CLARABD para el lenguaje R (23) donde se utiliza
un agrupamiento de k-medoides y la implementa-
ción de la distancia de Gower que trabaja con da-
tos mixtos, al mismo tiempo que permite superar
la barrera de 65536 observaciones que actualmente
tiene el software para k-medoides.
En este contexto, la propuesta de este trabajo, SMO-
TEMD, permite balancear muestras desbalancea-
das con datos mixtos (de ahí el sufijo MD, de Mixed
Data, agregado a SMOTE) y superar la limitante de
65536 observaciones que tiene el software R para la
clase minoritaria.
II. MATERIALES Y MÉTODOS
SMOTEMD es una extensión del algoritmo SMO-
TE para datos mixtos al mismo tiempo que permite
trabajar con más de 65536 observaciones en la clase
minoritaria de los datos desbalanceados.
La tabla 1 muestra una matriz de confusión como
ejemplo para ilustrar SMOTEMD.
Realidad
Predicción 1 0
1 10 15
0 5 70
Tabla 1. Matriz de confusión
23
De la tabla 1 se puede obtener los siguientes indica-
dores de clasificación:
• Precisión = 80/(10+70)=80%
• Especificidad = 15/(15+70) = 18%
• Sensibilidad = 10/(10+5)=67%.
Una inspección ingenua de estos resultados toma-
ría en cuenta únicamente los resultados de la pre-
cisión, pese a que claramente un indicador más
adecuado para este ejemplo es la especificidad. Es
decir, debido a que se trata de datos no balanceados
(15% de observaciones igual a 1), se presenta una
paradoja en el indicador de precisión debido a que
es muy elevado, pero no recoge la realidad de los
datos analizados.
Para solventar este problema, SMOTE y SMO-
TEMD realizan un sobre muestreo de la clase
minoritaria (cuando la respuesta es igual a 1 en el
ejemplo) tal que se generan individuos sintéticos.
La figura 1 muestra el problema inicial, donde el
color rojo es la clase minoritaria.
Figura 1. Tiempo de Retardo y Dimensión de Encaje
Luego, la figura 2 muestra los individuos sintéticos
que son generados mediante combinaciones linea-
les convexas de los individuos más cercanos. De la
distancia que separa a los vecinos más cercanos se
toma un valor aleatorio con distribución uniforme
entre 0 y 1 para obtener observaciones sintéticas
(puntos rojos ubicados sobre las lineas de los datos
originales).
Figura 2. Dispersión de puntos que ilustra la clase minoritaria y la
generación de datos sintéticos
El algoritmo SMOTE únicamente permite trabajar
con datos numéricos, mientras que con SMOTEMD
es posible usar datos mixtos usando la distancia de
Gower. Esta distancia realiza una estandarización
específica para cada tipo de variable (cualitativa o
cuantitativa) y luego se calcula un promedio de to-
das las variables estandarizadas (24).
III. RESULTADOS
Para estudiar la propuesta SMOTEMD, se realizan
dos escenarios de simulación. En el primer expe-
rimento de simulación se evalúa la sensibilidad y
especificidad de los modelos: logit, corrección de
constante y SMOTEMD. En el segundo experi-
mento se realizan varias estimaciones del estadísti-
co Kolmogorov Smirknov (KS) para tener una refe-
rencia del poder de discriminación de SMOTEMD.
Simulación A
En este experimento se simulan 50000 datos con
dos covariables categóricas donde la tasa de respues-
ta de la variable dependiente es 1.6% que represen-
ta los datos no balanceados. Esta configuración se
itera 1000 veces para obtener distribuciones de los
indicadores estudiados. Las figuras 3 y 4 muestran
los resultados de los indicadores de sensibilidad y
especificidad para los modelos logit (Original), co-
rrección de constante (Corregido) y SMOTEMD.
Figura 3. Densidad del indicador de sensibilidad
Figura 4. Densidad del indicador de especicidad
Morales, Moreta, Morales

24
ISSN 2477-9105 Número 24 Vol.1 (2020)
La tabla 2 muestra los promedios de cada indicador.
Orig. Correg. SMOTEMD
Sen 0.992 0.998 0.934
Esp 0.717 0.1452 0.926
Tabla 2. Promedio de indicadores de Sensibilidad (Sen) y
Especicidad (Esp).
Por un lado, se puede apreciar que el indicador
de sensibilidad es ligeramente menor para SMO-
TEMD. Por otro lado, la ganancia adquirida en es-
pecificidad es muy superior que sus competidores.
Al comparar estas evidencias, se puede concluir
que SMOTEMD es un algoritmo superior para tra-
bajar con datos desbalanceados.
Simulación B
En este experimento se simulan 100000 datos con
cinco covariables numéricas donde la tasa de res-
puesta de la variable dependiente es 0.1%, 2.1% y
6.1% que representa los datos no balanceados y se
puede apreciar la sensibilidad de los métodos ante
cambios en la tasa de respuesta. Esta configuración
se itera 300 veces para obtener distribuciones del
estadístico KS para evaluar el poder de discrimina-
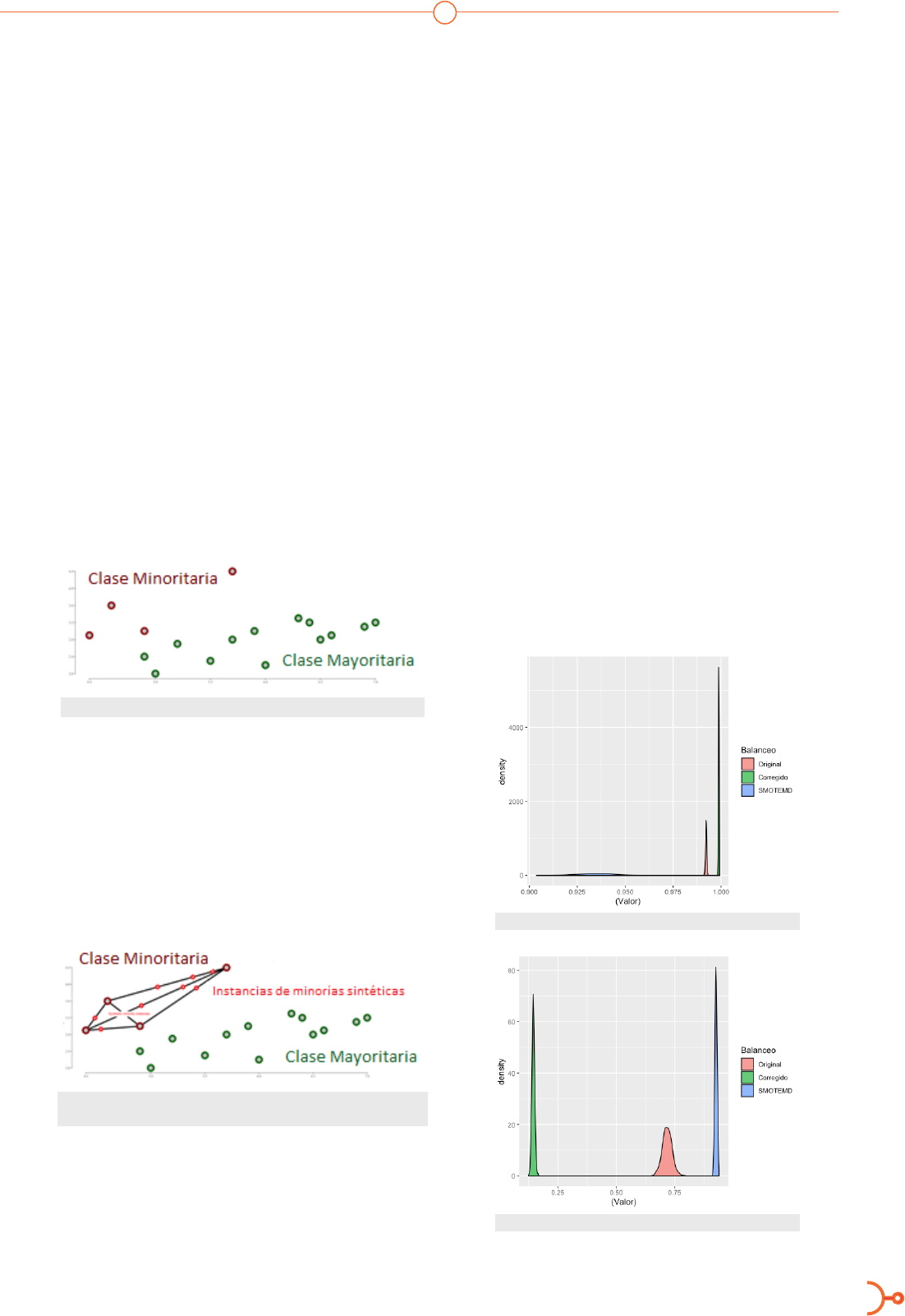
ción de los métodos. Las figuras 5, 6 y 7 muestran
los resultados para cada tasa de respuesta.
Figura 5. Histograma del estadístico KS con
tasa de respuesta 0.1%
Figura 6. Histograma del estadístico KS con
tasa de respuesta 2.1%
Figura 7. Histograma del estadístico KS con
tasa de respuesta 6.1%
La figura 5 muestra que, para una tasa de respues-
ta de 0.1%, SMOTEMD tiene valores menores que
SMOTE y ligeramente superior al enfoque logit
(Original). Las figuras 6 y 7 favorecen al algoritmo
SMOTEMD debido a que el KS resultante es mayor
o presenta menor varianza que sus competidores.
IV. DISCUSIÓN
La simulación 1 se alinea con los resultados obte-
nidos en (10) debido a que los indicadores de sen-
sibilidad y especificidad son mejores al usar SMO-
TEMD.
La eficiencia computacional de SMOTEMD depen-
de de, al menos, dos elementos. Por un lado, si se
trabaja con menos de 65536 observaciones, el tiem-
po de cómputo está acotado por la eficiencia del cál-
culo de la distancia de Gower en R. Por otro lado,
al superar este número de observaciones, depen-
de del número de submuestras y su tamaño. Esto
puede ser potenciado mediante el uso de funciones
wrappers donde se use lenguajes de más bajo nivel
como C o Fortran.
Se pudo apreciar que SMOTEMD tiene un ren-
dimiento ligeramente mejor en tasas de respuesta
pequeñas. Esto puede deberse al proceso de estan-
darización que tienen las variables ayudando a la
reducción de la volatilidad observada.
Un posible escenario desvaforable para SMO-
TEMD es el aumento en la tasa de respuesta. Tal
parece que, al aumentarla, se aprecia cada vez
menos su diferencia con el algoritmo tradicional
SMOTE. No obstante, el manejo de datos mixtos
de SMOTEMD seguiría siendo un aporte.
Cabe indicarse que, para efectos de replicabilidad,
el código de programación para obtener los resulta-
dos de ambas simulaciones se encuentran disponi-
bles en https://github.com/vmoprojs/ArticleCodes.
V. CONCLUSIONES
Se ha mostrado la superioridad del algoritmo
SMOTEMD en cuanto a sensibilidad y especifici-
dad. Esta propiedad es heredada de manera directa
por SMOTE.
En el caso de que se requiera balancear los datos
para realizar predicciones, en términos generales
el estadístico KS que se estudia en la simulación 2
presenta mejores propiedades en SMOTEMD que
sus competidores, tanto en media como en varian-
za. No obstante, para el escenario donde la tasa de

25
R
eferencias
1. W. Wei , J. Li, L. Cao, Y. Ou y J. Chen, Eective detection of sophisticated online banking fraud on
extremely imbalanced data, World Wide Web. 2013: 449–475.
2. P. Van Deusen y L. Irwin, A robust weighted EM algorithm for use-availability. Environ Ecol Stat.
2012: 205–217.
3. G. King y L. Zeng , Logistic Regression in Rare Events Data. e Socieciety For Political Methodo-
logy, 9 (2) 2001. 137-163.
4. B. Kitchenham, A procedure for analyzing unbalanced datasets. IEEE transactions on Soware
Engineering, 24 (4) 1998: 278-301.
5. B. Baesens, V. Van Vlasselaer y W. Verbeke, Fraud analytics using descriptive, predictive, and social
network techniques: a guide to data science for fraud detection, Estados Unidos: John Wiley & Sons, 2015.
6. G. M. Weiss, Mining with rarity: a unifying framework. ACM SIGKDD Explorations Newsletter.
2004: 7-19.
7. A. P. Bradley, e use of the area under the ROC curve in the evaluation of machine learning algo-
rithms. Pattern recognition, 30 (7) 1997: 1145-1159.
8. H. He, Y. Bai, E. A. Garcia y S. Li, ADASYN: Adaptive Synthetic Sampling Approach for Imbalan-
ced Learning. InternationalJoint Conference on Neural Networks. 2008: 1322-1328.
9. C. Drummond y R. C. Holte, C4.5, Class Imbalance, and Cost Sensitivity: Why Under-Sampling
beats Over-Sampling, de Workshop on learning from imbalanced datasets II, Washington, DC: Citeseer.,
2003.
10. N. V. Chawla, K. W. Bowyer, L. O. Hall y W. Philip Kegelmeye, SMOTE: Synthetic Minority
Over-sampling Technique. Journal of Artificial Intelligence Research. 2002: 321–357.
11. C. Manski y S. Lerman, e Estimation of Choice Probabilities from Choice Based Samples. Eco-
nometrica 45, 1977.
12. H. He y E. A. Garcia, Learning from imbalanced data. IEEE Transactions on knowledge and data
engineering, 21 (9) 2009: 1263-1284.
13. C. Lynch, How do your data grow? Nature; 2008: 1-2.
14. J. Hurtado, . N. Taweewitchakreeya, . X. Kong y X. Zhu, A Classifier Ensembling Approach For
Imbalanced Social Link Prediction, de International Conference on Machine Learning and Applications,
2013.
15. H.-J. Yoon, Development of Contents on the Marine Meteorology Service by Meteorology and
Climate Big Data. e Journal of the Korea institute of electronic communication sciences. 2016: 125-138.
16. A. S. Shirkhorshidi, S. Aghabozorgi, T. . Y. Wah y T. Herawan, Big Data Clustering: A Review, de
Murgante B. et al. (eds) Computational Science and Its Applications – ICCSA 2014. ICCSA 2014, Cham,
2014.
17. Y. Sahin y E. Duman, Detecting credit card fraud by ANN and logistic regression, de 2011 Interna-
tional Symposium on Innovations in Intelligent Systems and Applications, Istanbul, IEEE, 201: 315-319.
18. B. Krawczyk, Learning from imbalanced data: open challenges and future directions. Prog Artif
Intell, 2016.
19. A. Fernández, V. López, M. Galar, M. J. del Jesus y F. Herrera, Analysing the classication of imba-
lanced data-sets with multiple classes: Binarization techniques and ad-hoc approaches. Knowledge-Based
Systems. 2013: 97-110.
20. B. W. Silverman y M. C. Jones, (1951): An important contribution to nonparametric discriminant
analysis and density estimation: Commentary on Fix and Hodges (1951). International Statistical Review/
Revue Internationale de Statistique, 57 (3) 1989: 233-238.
respuesta es de 0.1%, el algoritmo SMOTE original
es mejor.
Es importante notar que SMOTEMD puede ser
usado cuando se tiene más de 65536 observaciones,
lo cual es una propiedad que lo enmarca en un con-
texto Big Data en R.
VI. AGRADECIMIENTOS
Los autores agradecen al grupo de investigación
Data Science Research Group CIDED de la Escuela
Superior Politécnica de Chimborazo. Víctor Mora-
les-Oñate y Bolívar Morales-Oñate pertenecen al
grupo.
Morales, Moreta, Morales

26
ISSN 2477-9105 Número 24 Vol.1 (2020)
21. P. Skryjomski y B. Krawczyk, Influence of minority class instance types on SMOTE imbalanced
data oversampling, Proceedings of Machine Learning Research. 2017: 7-21.
22. V. Morales Oñate y B. Morales Oñate, A robust clustering technique for a Big Data approach: CLA-
RABD for Mixed data types. Perles, 2019.
23. R. C. Team, R: A language and environment for statistical computing, Vienna, 2014.
24. B. Borra, T. Rohit y D. Nilanjan, Satellite Image Analysis: Clustering and Classication, de Satellite
Image Analysis: Clustering and Classication, Estados Unidos, Springer, 2019: 53-81.
25. B. Bischl, M. Lang, L. Kottho, J. Schiner, J. Richter, E. Studerus, G. Casalicchio y Z. Jones, Open-
ML: An R package to connect to the machine learning platform OpenML. Journal of Machine Learning
Research. 17(170) 2016: 1-5.