
54
ISSN 2477-9105 Número 24 Vol.1 (2020)
R
esumen
Una aproximación para entender los fenómenos con dinámica compleja es el análisis de datos. El
escalado multidimensional permite visualizar el comportamiento de los sistemas y capturar su evolución
espaciotemporal. Mientras que el cálculo fraccional, aplicado mediante Fractional State Space Portrait
permite identificar clústeres en grupos de datos, incluyendo variables meteorológicas como la temperatura.
Para ello se ha utilizado la información mutua multivariante para encontrar el orden de derivada óptima
que ha dado como resultado una visualización mejorada del sistema dinámico de temperaturas en 11
estaciones meteorológicas de la provincia de Chimborazo durante el año 2015. En el mapa del Fractional
State Space Potrait se ha logrado identificar dos grandes clústeres que representan las dos estaciones típicas
de un clima tropical ecuatorial. Tales clústeres se encuentran fuertemente influenciados por los diversos
microclimas presentes en un territorio heterogéneo.
Palabras clave: Escalado Multidimensional, Retrato Fraccional Estado Espacial, Chimborazo.
A
bstract
Data analysis is an approach to understand phenomena with complex dynamics. Multidimensio-
nal Scaling allows the visualization of systems behavior and also captures its space-time evolution.
While fractional calculation, applied through Fractional State Space Portrait permits to identify
clusters in data groups, including meteorological variables such as temperature. Aimed at this, the
mutually multivariate information has been used to find the optimal derivative order that has re-
sulted in an improved revealing of the dynamic temperature system in 11 meteorological stations
in the province of Chimborazo during 2015. On the map of the State Space Fractional Portrait
two large clusters that represent the two typical seasons of an equatorial tropical climate can be
identified. Such clusters are strongly influenced by the numerous microclimates present in this
heterogeneous territory.
Keywords: Multidimensional Scaling, Fractional State Space Portrait, Chimborazo.
APLICACIÓN DEL CÁLCULO FRACCIONAL A UNA SERIE DE
TEMPERATURAS DE LA ZONA ANDINA.
Application of fractional calculus to a series of temperatures of the Andean zone.
1
Cristina Ramos Araujo*,
2
Hitler Guerrero Hidalgo,
1
Escuela Superior Politécnica de Chimborazo ESPOCH, Riobamba, Ecuador
2
Universidad Regional Amazónica IKIAM, Tena, Ecuador
*cristinaestefaniaramos@gmail.com
Fecha de recepción: 27-08-2019 Fecha de aceptación: 25-06-2020 Fecha de publicación: 30-07-2020
I. INTRODUCCIÓN
El análisis de datos ha sido empleado como he-
rramienta en la investigación cientíca para
entender la dinámica de fenómenos comple-
jos mediante el uso de herramientas matemáti-
cas y estadísticas. El escalado multidimensional
(MDS) permite visualizar el comportamiento de
los sistemas y capturar la evolución espaciotem-
poral (1), (2). El método permite identicar dife-
rentes particularidades de datos, agrupando con
parámetros apropiados (3). Junto con la trans-
formada de Fourier, MDS ha sido empleado para
identicar patrones en variables económicas (4).

55
El cálculo fraccional (CF) amplía la perspectiva
de las investigaciones, en donde se ha aplicado
Fractional State Space Portrait (FSSP) para iden-
ticar clústeres en grupos de datos macroeconó-
micos y bursátiles (5). Sin embargo, la aplicación
de estos métodos no se limita exclusivamente al
campo económico, es aplicable en ciencias am-
bientales donde se requiera encontrar patrones
que marquen trayectorias de comportamiento
en sistemas dinámicos, tal es el caso de las varia-
bles meteorológicas como la temperatura, donde
Machado sugiere adoptar la información mutua
multivariante para proponer un orden de deri-
vada óptima que ha dado como resultado una
visualización mejorada del sistema dinámico de
temperaturas en planeta Tierra. De manera aná-
loga se ha podido aplicar el método para revelar
patrones en otros sistemas dinámicos (6), (7), (8).
Ecuador es un país con gran potencial solar (9),
el cual se encuentra atravesado de norte a sur por
la cordillera de Los Andes que divide al país en
regiones naturales. En la región montañosa de la
sierra central se encuentra la provincia de Chim-
borazo, en donde se ha instalado una red de es-
taciones meteorológicas automáticas, las cuales
han medido y transmitido datos atmosféricos
desde su instalación en 2013. Desde entonces
se han desarrollado estudios (10) y (11) en los
cuales se han determinado las relaciones lineales
empleando el coeciente de Pearson y a la vez se
han creado modelos para la estimación de otras
variables meteorológicas (12). Sin embargo, el
análisis de linealidad se vuelve insuciente para
comprender un sistema tan complejo como el
meteorológico, para el cual se requiere estableces
las relaciones ocultas entre sus diferentes varia-
bles.
Para tal propósito, los autores emplean el con-
cepto de cálculo fraccional mediante el FSSP en
una serie de temperaturas de 365 días del año
2015, procedente de 11 estaciones meteorológi-
cas distribuidas en la provincia de estudio. Estos
datos se interpretan como un sistema dinámico
con evolución espaciotemporal correspondiente
a cada estación durante el año de estudio, tales
variables a su vez forman subsistemas relacio-
nados entre ellos (6). Una vez obtenido el orden
óptimo de la derivada, se realizó la comparación
entre FSSP y MDS para contrastar la represen-
tación visual del comportamiento dinámico del
sistema.
II. MATERIALES Y MÉTODOS
La provincia de Chimborazo está situada en la
parte central de Ecuador. Su territorio se extiende
en 6500 km2 desde la región trópica a 156 metros
sobre el nivel del mar hasta la cima del volcán
Chimborazo a 6268 m.s.n.m. (13). Está atravesa-
da por la Cordillera de los Andes y drenada por
las subcuencas del río Guayas y el Pastaza. Una
red de 11 estaciones meteorológicas automáticas
ha sido instalada desde 2013 en toda la región.
Las estaciones han medido datos como: tempera-
tura del aire y suelo [°C], humedad relativa [%],
presión atmosférica [hPa], radiación global y di-
fusa [Wm
-2
], velocidad de viento [ms
-1
]. La pro-
vincia de Chimborazo posee una topografía muy
variable que, en conjunto con su ubicación en el
centro del país, permite la formación de 13 eco-
sistemas (14) y de una diversidad de microclimas
en los sitios donde se encuentran distribuidas las
estaciones meteorológicas, el detalle de la ubica-
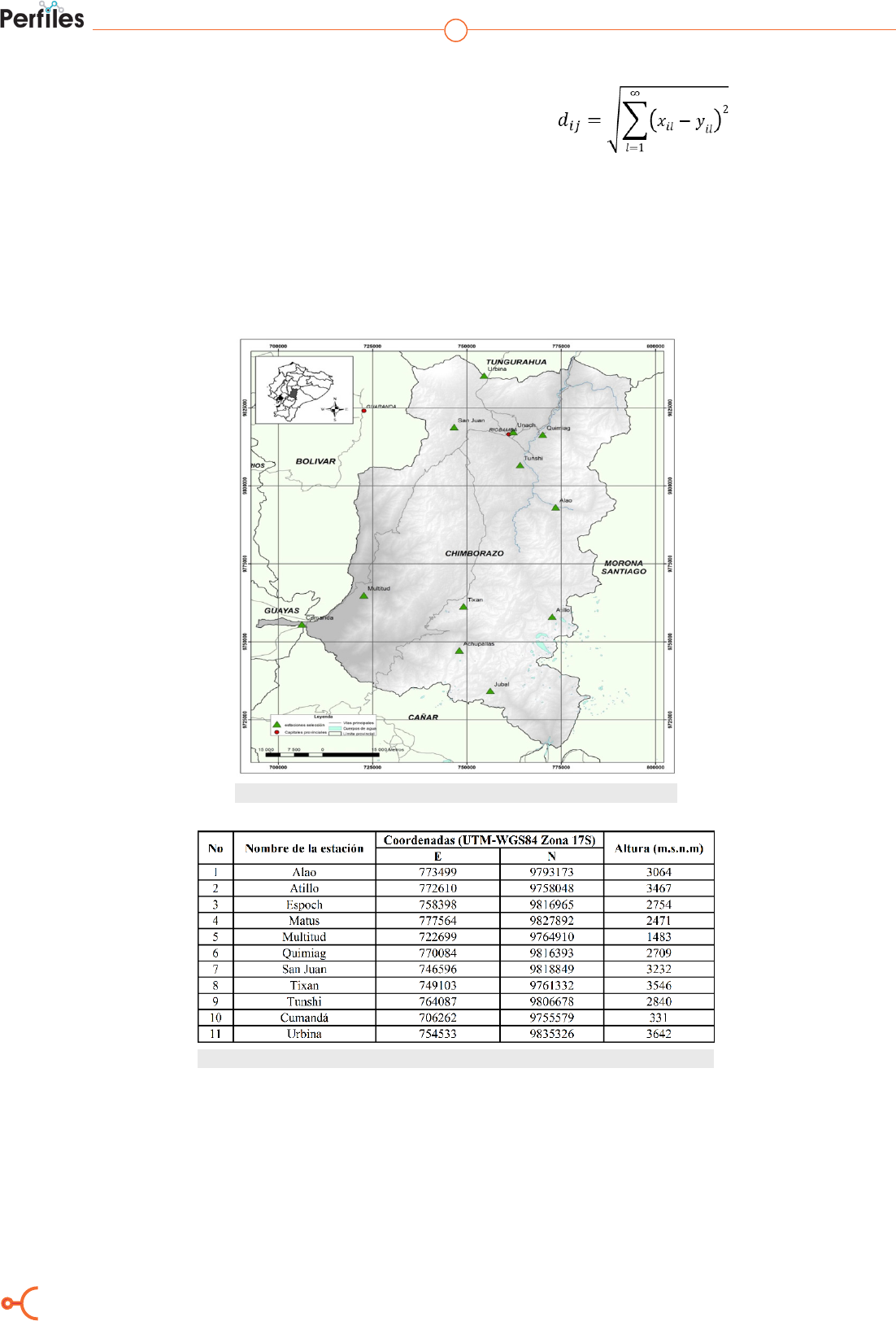
ción puede ser observado en la Figura 1.
Para este estudio se ha elegido manejar prome-
dios diarios de temperatura del aire [ºC], para
visualizar el comportamiento del clima en el año
2015. Esta selección tiene el 98.2% de los datos
mientras que su complementario corresponde a
datos faltantes. Se ha utilizado algunos modelos
de transmitancia atmosférica y otros basados en
imágenes satelitales creados para la zona Andi-
na con el propósito de completar la información
(10) y (11).
Los datos son interpretados como un sistema di-
námico complejo de la evolución de las tempe-
raturas a través del tiempo. Se considera la serie
de tiempo de temperaturas en cada estación me-
teorológica i (i=1,2,…,n) como el estado de la va-
riable y
i
(t) de un conjunto de n=11 subsistemas
dinámicos posiblemente conectados, donde t re-
presenta el tiempo (6). En este estudio se utiliza
métodos numéricos, estadísticos y computacio-
nales para representar el comportamiento diná-
mico de las temperaturas aplicando dos distintos
métodos de visualización MDS y FSSP.
Ramos, Guerrero
56
ISSN 2477-9105 Número 24 Vol.1 (2020)
Análisis de escalado multidimensional (MDS)
MDS es una técnica estadística utilizada para re-
ducir la dimensión de datos multivariantes para
obtener una representación espacial. Tiene una
amplia aplicación en medicina, psicología, eco-
nomía, geofísica y climatología (4), (5) y (6). En
este método las similitudes entre pares de objetos
son representadas por las distancias Euclidianas
ecuación 1, también denominada solución clási-
ca.
(1)
La interpretación de los resultados es la forma-
ción de conjuntos de acuerdo a la distancia entre
los puntos en el mapa. Empleando soware esta-
dístico RStudio con paquetes adicionales se han
generado grácas interactivas en 2 y 3 dimensio-
nes.
Figura 1. Ubicación de las estaciones meteorológicas en la provincia de Chimborazo
Tabla 1. Ubicación de las estaciones en la provincia de Chimborazo
Un sistema k-dimensional se puede representar
mediante un conjunto de ecuaciones diferencia-
les de primer orden que rigen las k variables del
estado y
1
(t),y
2
(t),…,y
k
(t). Dichas ecuaciones se
obtienen de la relación funcional entrada-salida
del sistema para un conjunto dado de variables
de estado. Conociendo y
1
(t),y
2
(t),…,y
k
(t) en
el momento t≥t
0
y las entradas del sistema para
t≥t
0
. El espacio de estado consiste en el conjunto
de todos los estados posibles, cada uno corres-
pondiente a un punto único. A medida que evo-
luciona, obtenemos secuencias de puntos que
describen trayectorias en el espacio de estados
el conjunto de las trayectorias es el SSP. Para los

57
sistemas de primero, segundo y tercer orden,
se puede representar (SSP) y se puede inferir el
comportamiento del sistema a partir de la corres-
pondiente representación gráca (5), (6) y (15).
Se ha utilizado series de tiempo y
i
(t) con sus
derivadas de orden entero (k-1), k Î ℝ con res-
pecto al tiempo, que se pueden denominar varia-
bles de fase. A continuación, se puede construir
el SSP. La representación k-dimensional es com-
pleja porque el orden hipotético del modelo di-
ferencial es desconocido. Se necesita determinar
el orden óptimo de las derivadas con respecto al
tiempo. Se conoce que los datos atípicos k-di-
mensionales son difíciles de separar en una base
de datos (16) (17), lo cual conlleva a un trabajo
exhaustivo para calcular las distancias entre cada
par de variables y a la vez aplicar alguna técnica
para detectar valores anómalos multivariantes.
Para tal efecto, se ha aplicado diferencias numé-
ricas para datos o funciones ruidosas, emplean-
do el algoritmo propuesto por Holoborodko (18)
donde h es el periodo de muestra.
(2)
(3)
Medida de información mutua.
Como parte de la Teoría de Información se puede
encontrar la denición de la Información Mutua
de variables que mide la dependencia estadística
mutua entre dos variables aleatorias. La Informa-
ción mutua de dos variables aleatorias discretas
X, Y se dene como (19):
(4)
Donde p(x), p(y) representan las probabilidades
marginales de las variables aleatorias X,Y, ade-
más p(x,y), representa la distribución conjunta
de las variables aleatorias X,Y. (6), (20). Para el
presente artículo se utiliza la Información Mutua
Normalizada en referencia a (21):
(5)
Donde H(X) y H(Y), representan la entropía.
(6)
La información mutua normalizada tiene la ven-
taja de simplicar la comparación entre diferen-
tes condiciones y mejorar la sensibilidad.
Cálculo fraccional (CF)
El CF puede ser empleado como una extensión
del Cálculo Diferencial e Integral. En la siguiente
ecuación , p puede tomar cualquier valor,
sea este positivo, negativo, real o imaginario; en-
tonces se convierte en un poderoso recurso para
el análisis de datos (22).
En este estudio se ha empleado cálculo numérico
y analítico para resolver un sistema fraccional. Se
menciona la ecuación diferencial de orden frac-
cionario en ecuación 7.
(7)
Con condiciones iniciales y
β
(0)=0 ; y(0)=0
Como una aproximación de las derivadas frac-
cionales de la ecuación 5 se utiliza métodos nu-
méricos en relación a la ecuación 7 con el prin-
cipio de “memoria a corto plazo” formulada por
(23)
(8)
Donde L es la longitud de memoria y h es la fre-
cuencia de tiempo.
(9)
El coeciente binomial está dado por
donde b
0
=1
Favorablemente, según (23), también se puede
calcular una aproximación de un sistema diná-
mico fraccional con sistemas de tipo entero de la
siguiente manera en la ecuación 7.
(10)
Ramos, Guerrero
58
ISSN 2477-9105 Número 24 Vol.1 (2020)
Los coecientes de a
i
k
del sistema dinámico de
orden entero toman los siguientes valores
a
i
2
=0.7414; a
i
1
=0.2313; a
i
0
=1 que han sido cal-
culados por el método de mínimos cuadrados
Fractional state space portrait (FSSP)
Para la construcción del FSSP el orden de la de-
rivada no se limita a un número entero, propor-
cionando una alternativa valiosa para obtener
la representación de las relaciones entre las va-
riables del sistema k-dimensional, visualizando
características escondidas y no capturadas por
otros métodos (8).
Como primer paso para construir el FSSP se cal-
cula el orden óptimo de la derivada, para el sis-
tema dinámico (6). Posteriormente se emplea las
ecuaciones 8 y 9 para obtener la representación
del cambio de estado de cada variable.
Una vez obtenidas, las grácas arrojadas por
MDS y FSSP se comparan buscando la represen-
tación adecuada.
III. RESULTADOS
Análisis de Escalado Multidimensional
El conjunto de datos es representado por las me-
diciones de temperatura de 365 días en el año
2015 en una proyección de escalado multidimen-
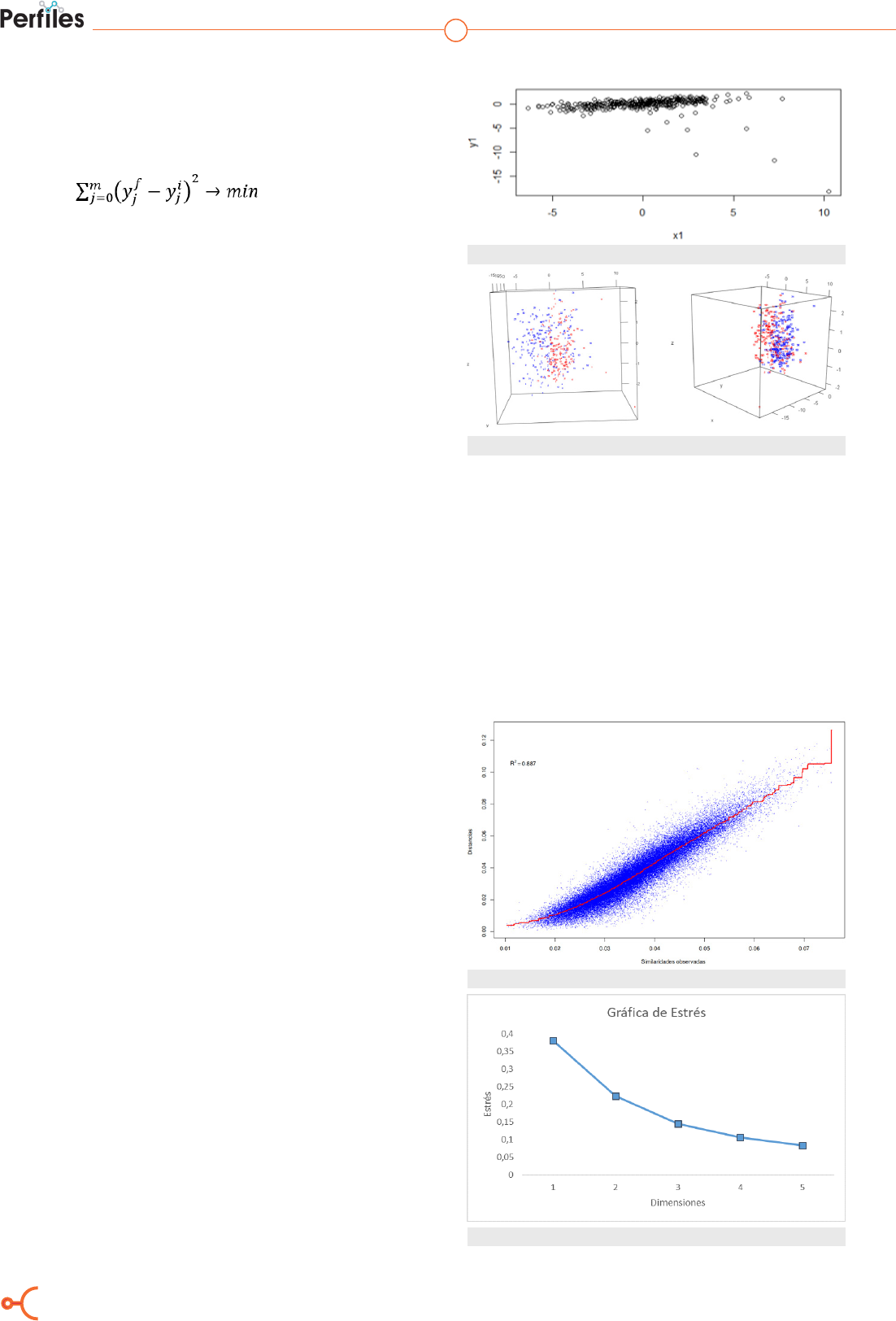
sional para u = 2 que se muestra en la Figura 2,
donde cada punto representa las mediciones de
la temperatura durante un tiempo t.
Las distancias cortas entre dos puntos en el mapa
signican que las correspondientes mediciones
son similares, mientras que las distancias largas
entre los puntos representan menor similitud en-
tre sí.
La Figura 3 muestra el escalado multidimensio-
nal para u = 3, donde se puede apreciar dos gru-
pos semi denidos que representan las dos esta-
ciones del año típicas de la zona ecuatorial: los
días secos y lluviosos representados con puntos
rojos y azules respectivamente.
Figura 2. Escalado multidimensional para u=2
Figura 3. Escalado multidimensional para u=3
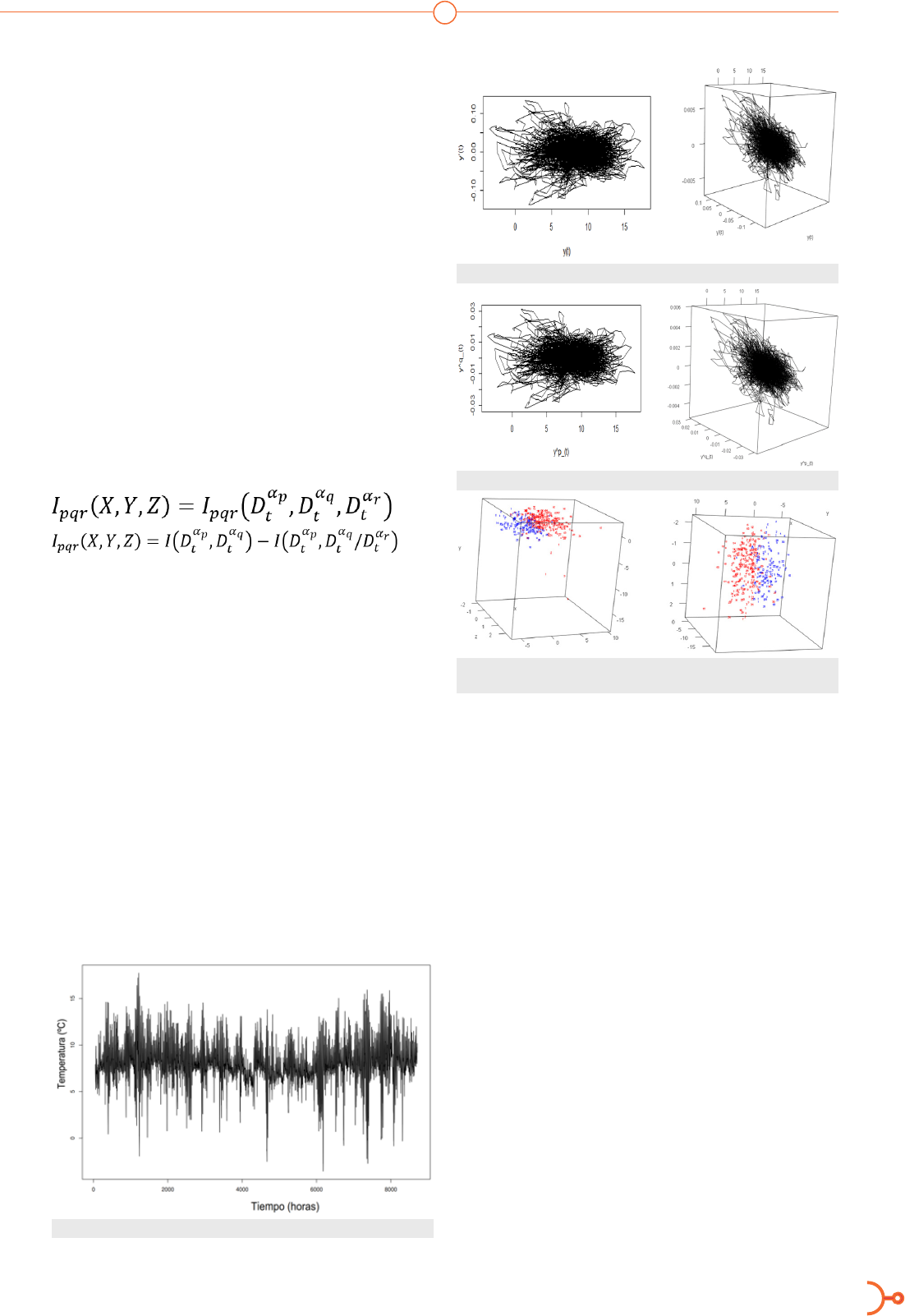
En la Figura 4 se observa el gráco Sherpad en
2 dimensiones, donde se identica que las simi-
laridades y las distancias tienen una fuerte rela-
ción. El coeciente de determinación R
2
=0.89,
que signica que el 89% de la variabilidad de las
distancias y las similaridades esta explicada. Se
ha obtenido la estructura de mejor ajuste de los
puntos de análisis MDS, el cual tiene el menor
estrés a medida que las dimensiones aumentan
como se observa en la Figura 5.
Figura 4. Sherpad Plot.
Figura 5. Gráca de Estrés.
59
Análisis SSP
Se ha generado el SSP de la serie de tiempo de
temperaturas, se observa en la Figura 6 que la
variable es una serie estacionaria anual. Sin em-
bargo utilizando las ecuaciones 2 y 3 se puede
observar el cambio de estados y(t), y'(t), y''(t) de
las temperaturas plasmado en la Figura 7. La pe-
riodicidad no es evidente durante los cambios de
estado representados en la gráca.
Análisis FSSP
Para determinar el orden de las derivadas del
FSSP para la i
th
estación meteorológica, se ha
comparado s=72 valores de orden α de D
α
t
{y
i
(t)}
que corresponden a discretizaciones numéricas
en un intervalo de αÎ[0;2]. Para llevar a cabo este
procedimiento primero se ha calculado la Infor-
mación mutua multivariante descrita por (24).
(11)
(12)
Como segundo paso se elige el orden óptimo
de derivada que corresponde al mínimo valor
de I
pqr
(X,Y,Z), como lo sugiere Machado (6). Se
observa en la Figura 8 la gráca para tres dimen-
siones del FSSP para el óptimo orden de derivada
{α
p
,α
q
,α
r
}={0.02;0.70;1.52}. Los grácos presen-
tan una semejanza con los obtenidos empleando
órdenes entero en la Figura 7.
Los grupos obtenidos por los dos métodos son
aparentemente similares, sin embargo, la gráca
del FSSP (Figura 9) representa grupos de tempe-
ratura mejor denidos; de esta manera, el méto-
do FSSP se presenta como una buena alternativa
para discretizar variables meteorológicas como
temperaturas.
Figura 6. Temperaturas en función del tiempo.
Figura 7. SSP de la Estación Atillo.
Figura 8. FSSP Temperaturas Atillo
Figura 9. Representación de los clústeres basados en {α
p
,α
q
,α
r
}={0.02; 0.70;
1.52 }, para n=11 estaciones meteorológicas.
IV. DISCUSIÓN
Para la construcción del FSSP se ha obtenido el
óptimo orden de derivada {α
p
,α
q
,α
r
} = {0.02; 0.70;
1.52} en comparación con Machado (6) {α
p
,α
q
,α
r
}
= {0.029; 0.53; 1.33}. Los valores no tienen una
diferencia signicativa entre sí, pero se obtiene
un criterio de visualización de comportamiento
de las Temperaturas.
En el mapa FSSP (Figura 9), se puede apreciar
dos grupos que representan las dos estaciones
del año denidas para la zona ecuatorial: los días
secos en rojo y los días lluviosos en azul. Las
temperaturas en climas tropicales se caracterizan
por tener variaciones diarias más grandes que las
variaciones anuales. Esto es típico en el Ecuador
que no posee estaciones termales, además carece
de un invierno largo en el cual la actividad bio-
lógica se reduzca por las temperaturas bajas. La
cordillera de los Andes es el factor más inuyente
que genera complejos patrones espaciales de pre-
Ramos, Guerrero

60
ISSN 2477-9105 Número 24 Vol.1 (2020)
cipitación, afectadas por las cuencas del Pacíco
y del Amazonas. Las masas de aire provenientes
del Océano Pacíco ejercen su inuencia en las
laderas occidentales de la cordillera, mientras
que las pendientes orientales están dominadas
por corrientes de aire húmedo que provienen del
Atlántico y la cuenca del Amazonas (25), (26). En
los valles interandinos las masas de aire oceáni-
cas y continentales se encuentran, formando dos
estaciones climáticas en la zona: días lluviosos de
febrero a mayo y octubre y noviembre; días se-
cos en el periodo de junio a septiembre, el cual es
más pronunciado que el segundo periodo alrede-
dor de diciembre (25).
La provincia de Chimborazo no se caracteriza
por su uniformidad topográca, altitudinal, ni
climática. Su conguración biogeográca hace
posible la formación de 13 ecosistemas en su te-
rritorio (14). La formación de microclimas con
diferente precipitación y humedad relativa per-
mite que no se observe una diferenciación muy
marcada entre las estaciones, lo cual es visible
en la Figura 9, donde los clústeres se encuentran
muy cercanos entre sí.
V. CONCLUSIONES
Al aplicar el Análisis de Escalado Multidimien-
sional se ha podido identicar dos grupos no
delimitados, los cuales se les ha asociado a días
secos y lluviosos. La gráca de Sherpad indica
que el 89% de la variabilidad de los datos están
explicados por el modelo en tres dimensiones.
Se compararon los 72 valores de orden α que
corresponden a discretizaciones numéricas en
un intervalo α Î [0,2]. De la comparación se ha
empleado los valores menores resultantes. Estos
valores forman el orden de derivada óptimo para
la construcción del FSSP. Se ha comparado con
el orden de derivada entero y se ha determinado
que no tienen una diferencia signicativa.
La aplicación de FSSP funciona como una herra-
mienta útil para discretizar el conjunto de datos
y mejorar la representación visual del sistema di-
námico. Al comparar la Figura 3 con la Figura
9, en esta última se puede observar con mayor
claridad dos grupos: días secos y días lluviosos; el
mejor método evaluado en el estudio para inter-
pretar el sistema dinámico de las temperaturas de
11 estaciones meteorológicas en la provincia de
Chimborazo en el año 2015 es el FSSP.
VI. AGRADECIMIENTOS
Al Centro de Energías Alternativas y Ambiente
CEAA ESPOCH por proporcionar los datos em-
pleados para la presente investigación.
Al Dr. Krisztián Kósi Ph.D. y al Prof. Dr. habil.
József K. Tar D.Sc. quienes colaboraron con sus
conocimientos.
R
eferencias
1. Tenreiro Machado J, Lopes AM, Galhano AM. Multidimensional scaling visualization
using parametric similarity indices. Entropy. 2015; 17(4): p. 1775-1794.
2. Huang JJ, Tzeng GH, Ong CS. Multidimensional data in multidimensional scaling using
the analytic network process. Pattern Recognition Letters. 2006; 26(6): p. 755–767.
3. Kósi K. Method of data center classifications. Acta Polytechnica Hungarica. 2012; 9(4): p.
127–137.
4. Machado JT, Duarte FB, Duarte DM. Analysis of financial data series using fractional fou-
rier transform and multidimensional scaling. Nonlinear Dynamics. 2011; 65(3): p. 235–245.
5. Machado , Mata ME, Lopes AM. Fractional state space analysis of economic systems. En-
tropy. 2015; 17(8): p. 5402–5421.
6. Machado J, Lopes AM. Fractional state space analysis of temperature time series. Fractio-
nal Calculus and Applied Analysis. 2015; 18(6): p. 1518–1536.
7. Namias V. The fractional order Fourier transform And its aplication to quantum mecha-
nics. IMA Journal of Applied Mathematics. 1980; 25(3): p. 241-265.
8. Lopez A, Tenreiro Machado J. State space analysis of forest fires. Journal of Vibration and
Control. 2016; 22(9): p. 2153-2164.

61
Ramos, Guerrero
9. Baigorria GA, Villegas EB, Trebejo I, Carlos JF, Quiroz R. Atmospheric transmissivity: dis-
tribution and empirical estimation around the central andes. International Journal of Climatology.
2004; 24(9): p. 1121–1136.
10. Recalde C, Cisneros C, Vaca D, RAMOS C. Relación de la transmitancia atmosférica con la
heliofanía y la diferencia de temperaturas extremas diarias en la zona ecuatorial andina. Informa-
ción tecnológica. 2015; 26(1): p. 143–150.
11. Ramos C, Perez N, Villacreses G, Vaca D, Chavez E, Perez M. Atmospheric transmisivity:
a model Comparison for equatorial andean highlands zone. Perfiles. 2016; 2(16): p. 6-13.
12. Haro S, Escudero A. Interpolación de datos faltantes mediante splint cúbico y mínimos
cuadrados. Perfiles. 2017; 1(17): p. 63-66.
13. Instituto Geofísico de la Escuela Politécnica Nacional. Instituto Geofísico - EPN. [Online].;
2019 [cited 2019 10 07. Available from: HYPERLINK "https://www.igepn.edu.ec/chimborazo" ht-
tps://www.igepn.edu.ec/chimborazo .
14. Ministerio de Ambiente Ecuador. Subsecretaría de Patrimonio Natural. [Online].; 2013 [ci-
ted 2019 10 07. Available from: HYPERLINK "http://app.sni.gob.ec/sni-link/sni/PDOT/NIVEL%20
NACIONAL/MAE/ECOSISTEMAS/DOCUMENTOS/Sistema.pdf" http://app.sni.gob.ec/sni-
link/sni/PDOT/NIVEL%20NACIONAL/MAE/ECOSISTEMAS/DOCUMENTOS/Sistema.pdf .
15. Willems JC, Polderman JW. Introduction to mathematical systems theory: a behavioral
approach. Springer Science & Business Media. 2013; 26.
16. Craven P, Wahba G. Smoothing noisy data with spline functions. Numerische Mathematik.
1978; 31(4): p. 377–403.
17. Diethelm K. An algorithm for the numerical solution of differential equations of fractional
order. Electronic transactions on numerical analysis. 1997; 5(1): p. 1-6.
18. Holoborodko P. Pavel Holoborodko, Applied Mathematics and more. [Online].; 2008 [ci-
ted 2018 Octubre 1. Available from: HYPERLINK "http://www.holoborodko.com/pavel/numeri-
cal-methods/numerical-derivative/smooth-low-noise-differentiators/" http://www.holoborodko.
com/pavel/numerical-methods/numerical-derivative/smooth-low-noise-differentiators/ .
19. Jaynes E. Information theory and statistical mechanics. Physical review. 1957; 106(4): p.
620-630.
20. Pham TH, Ho TB, Nguyen QD, Tran DH, Nguyen VH. Multivariate Mutual Information
Measures for Discovering Biological Networks. In 2012 IEEE RIVF International Conference on
Computing & Communication Technologies, Research, Innovation, and Vision for the Future;
2012; Ho Chi Minh City, Vietnam. p. 1-6.
21. Strehl A, Ghosh J. Cluster ensembles—a knowledge reuse framework for combining multi-
ple partitions. Journal of machine learning research. 2002; 3: p. 583–617.
22. Ylheng W, Yuquan C, Songsong C, Yong W. Discussion on fractional order derivatives.
IFAC-PapersOnLine. 2017; 50(1): p. 7002-7006.
23. Dorcak L. Numerical models for the simulation of the fractional-order control systems.
arXiv preprintmath/0204108. 2002.
24. Srinievasa S. A review on multivariate mutual information. In Univ. of Notre Dame; 2005;
Notre Dame, Indiana. p. 1-6.
25. Vuille , Bradley RS, Keimig F. Climate variability in the andes of ecuador and its relation to
tropical pacific and atlantic sea surface temperature anomalies. Journal of Climate. 2000; 13(14): p.
2520–2535.
26. Bendix J, Lauer W. Die niederschlagsjahreszeiten in ecuador und ihre klimadymamische
interpretation (rainy seasons in ecuador and their climate-dynamic interpretation). Erdkunde.
1992;: p. 118–134.